练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．在底面为正方形的四棱锥S-ABCD中，SA=SB=SC=SD，异面直线AD与SC所成的角为60°，AB=2．则四棱锥S-ABCD的外接球的表面积为（　　）
    A．6πB．8πC．12πD．16π

    分析 作出直观图，根据所给条件寻找外接球的球心位置，计算球的半径．

    解答 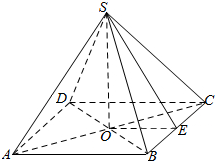解：取底面中心O，BC中点E，连结SO，SE，OE，则OE=$\frac{1}{2}AB$=1，OA=OB=OC=OD=$\sqrt{2}$，SO⊥平面ABCD，∴SO⊥OE，
    ∵AD∥BC，∴∠SCB为异面直线AD，SC所成的角，即∠SCB=60°，
    ∵SB=SC，∴△SBC是等边三角形，∵BC=AB=2，∴SE=$\sqrt{3}$，∴SO=$\sqrt{S{E}^{2}-O{E}^{2}}$=$\sqrt{2}$．
    ∴OA=OB=OC=OD=OS，即O为四棱锥S-ABCD的外接球球心．
    ∴外接球的表面积S=4π×（$\sqrt{2}$）2=8π．
    故选：B．

    点评 本题考查了球与内接多面体的关系，找出外接球的球心位置是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    6．双曲线的参数方程$\left\{\begin{array}{l}{x=\frac{a}{cosφ}}\\{y=btanφ}\end{array}\right.$中，参数的几何意义是什么？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知集合A={x|1≤x＜4}，B={x|x-a＜0}．
    （1）当a=3时，求A∩B，A∪B；
    （2）若A⊆B，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知（1+2x）n=$\sum_{k=0}^{n}$${C}_{n}^{k}$（2x）k=$\sum_{k=0}^{n}$αkxh（n∈N+），（1+2x）n的展开式中末三项的二项式系数的和为92，判断展开式系数组成的数列a0、a1，…，an的单调性，并求其最大项．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．有0、1、2、…、8这9个数字．
    （1）用这9个数字组成四位数，共有多少个不同的四位数？
    （2）用这9个数字组成四位密码，共有多少个这样的密码？
    （3）用这9个数字可以组成多少个无重复数字的四位数？
    （4）用这9个数字可以组成多少个无重复数字的四位偶数？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知sinα=$\frac{\sqrt{3}}{2}$，cosβ=$-\frac{1}{3}$，且tanα•tanβ＞0，则cos（α-β）的值是（　　）
    A．-$\frac{1-2\sqrt{6}}{6}$B．-$\frac{1+2\sqrt{6}}{6}$C．$\frac{1+2\sqrt{6}}{6}$D．±$\frac{1+2\sqrt{6}}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知直线x-y+3=0与圆心为（3，4）的圆C相交，截得的弦长为2$\sqrt{2}$．
    （1）求圆C的方程；
    （2）设Q点的坐标为（2，3），且动点M到圆C的切线长与|MQ|的比值为常数k（k＞0）．若动点M的轨迹是一条直线，试确定相应的k值，并求出该直线的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知直线y=x+b与两曲线C1：x2+y2-|x|-|y|=0和C2：x2+y2-|x|-|y|=$\frac{1}{2}$仅有两个交点，则实数b的取值范围是（　　）
    A．（-2，2）B．（-1-$\sqrt{2}$，1+$\sqrt{2}$）C．（-1-$\sqrt{2}$，-$\sqrt{2}$）∪（-$\sqrt{2}$，1+$\sqrt{2}$）D．（-1-$\sqrt{2}$，-2）∪（2，1+$\sqrt{2}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

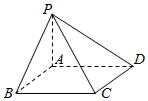    13．如图，四棱锥P-ABCD的底面是边长为4的正方形ABCD，侧棱PA垂直于底面，且PA=3．
    （1）求异面直线PB与CD所成的角的大小；（结果用反三角函数表示）
    （2）求四棱锥P-ABCD的体积．

    查看答案和解析>>

    同步练习册答案