
分析 由于双方获胜所能形成的比赛过程情况是相同的,只需考虑一方即可,由此可假设一方获胜,分别从(1)号、(2)号、(3)号、(4)号、(5)号棋手结束比赛这5种获胜的情况进分析解答即可.
解答 解:双方获胜所能形成的比赛过程情况是相同的,只需考虑一方.
假设一方获胜,获胜的情况又五大类:
(1)一号棋手结束比赛:连胜五盘,比赛过程只有1种;
(2)二号棋手结束比赛:他胜的场数可能是1、2、3、4、5,比赛过程有5种;
(3)三号棋手结束比赛:他胜的场数可能是1、2、3、4、5.
若胜1场:另外4场是1号或2号胜的,40、31、22、13、04,有5种比赛过程.
若胜2场:另外3场是1号或2号胜的,30、21、12、03,有4种比赛过程.
若胜3场:另外2场是1号或2号胜的,20、11、02,有3种比赛过程.
若胜4场:另外1场是1号或2号胜的,10、01,有2种比赛过程.
若胜5场:有1种比赛过程.
此类共有15种比赛过程.
(4)四号棋手结束比赛.他胜的场数可能是1、2、3、4、5.
若胜1场:另外4场是1号或2号或3号胜的,400、310、301、220、
211、202、130、121、112、103、040、031、022、013、
004,有15种比赛过程.
若胜2场:另外3场是1号或2号或3号胜的,300、210、201、120、
111、102、030、021、012、003,有10种比赛过程.
若胜3场:另外2场是1号或2号或3号胜的,200、110、101、020、
011、002,有6种比赛过程.
若胜4场:另外1场是1号或2号或3号胜的,100、010、001,有3种比赛过程.
若胜5场:有1种比赛过程.
此类共有35种比赛过程.
(5)五号棋手结束比赛.他胜的场数可能是1、2、3、4、5.
若胜1场:另外4场是1号或2号或3号或4号胜的,4000、3100、
3010、3001、2200、2110、2101、2020、2011、2002、1300、
1210、1201、1120、1111、1102、1030、1021、1012、1003、
0400、0310、0301、0220、0211、0202、0130、0121、
0112、0103、0040、0031、0022、0013、0004,共有35种赛过程.
若胜2场:另外3场是1号或2号或3号或4号胜的,
3000、2100、2010、2001、1200、1110、1101、1020、1011、1002、0300、
0201、0120、0111、0102、0030、0021、0012、0003,
共有20种比赛过程.
若胜3场:另外2场是1号或2号或3号或4号胜的,2000、1100、
1010、1001、0200、0110、0101、0020、0011、0002,共有10种比赛过程.
若胜4场:另外1场是1号或2号或3号或4号胜的,1000、0100、0010、0001,有4种比赛过程.
若胜5场:有1种比赛过程.此类共有70种比赛过程.
一方获胜共有:1+5+15+35+70=126种比赛过程,另一方获胜的比赛过程和中方相同,所以,共有126×2=252种不同的比赛过程.
故答案为:252.
点评 完成此类题目思路要清晰,根据所给条件中的逻辑关系进行认真分析.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
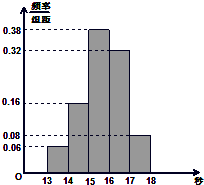 某学校1800名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),第五组[17,18],图是按上述分组方法得到的频率分布直方图.
某学校1800名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),第五组[17,18],图是按上述分组方法得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{500}{3}π$ | B. | $\frac{125}{6}π$ | C. | 100π | D. | 25π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com