
分析 (Ⅰ)当a=5时,不等式f(x)≥5x+1,即|2x-5|≥1,即 2x-5≤-1,或2x-5≥1,由此求得x的范围.
(Ⅱ)把要解的不等式等价转化为与之等价的两个不等式组,求出每个不等式组的解集,再取并集,即得不等式的解集,再根据不等式f(x)≤0的解集为{x|x≤-1},求得a的值.
解答 解:(Ⅰ)当a=5时,不等式f(x)≥5x+1,即|2x-5|+5x≥5x+1,即|2x-5|≥1,
即 2x-5≤-1,或2x-5≥1.
求得x≤2,或x≥3,故原不等式的解集为{x|x≤2,或x≥3}.
(Ⅱ)∵a>0,不等式f(x)≤0,即 $\left\{\begin{array}{l}{x≥\frac{a}{2}}\\{2x-a+5x≤0}\end{array}\right.$ ①,或 $\left\{\begin{array}{l}{x<\frac{a}{2}}\\{a-2x+5x≤0}\end{array}\right.$②.
解①可得$\frac{a}{2}$≤x<$\frac{a}{7}$,故①无解;解②可得x≤$\frac{a}{3}$,故原不等式的解集为{x|x≤$\frac{a}{3}$ }.
再根据已知原不等式的解集为{x|x≤-1},可得$\frac{a}{3}$=-1,∴a=-3.
点评 本题主要考查绝对值不等式的解法,体现了转化、分类讨论的数学思想,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
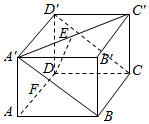 如图所示,在长方体ABCD-A′B′C′D′中,AB=λAD=λAA′(λ>0),E,F分别是A′C′和AD的中点,且EF⊥平面A′BCD′.
如图所示,在长方体ABCD-A′B′C′D′中,AB=λAD=λAA′(λ>0),E,F分别是A′C′和AD的中点,且EF⊥平面A′BCD′.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<m<$\frac{1}{3}$ | B. | 0<m≤$\frac{1}{3}$ | C. | $\frac{1}{3}$<m<1 | D. | $\frac{1}{3}$<m≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{8}$,+∞) | B. | ($\frac{1}{3}$,$\frac{{2\sqrt{2}}}{3}$) | C. | ($\frac{{\sqrt{2}}}{4}$,+∞) | D. | (2$\sqrt{2}$,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com