
分析 (Ⅰ)求出函数的导数,令h(x)=2x2-2ax+1,得到关于a的不等式组,解出即可;
(Ⅱ)求出函数的单调区间,根据二次函数的性质,求出f(x)的最大值,从而求出g(a)的表达式;
(Ⅲ)令x+2=$\frac{n+1}{n}$,则x=-$\frac{n-1}{n}$∈(-1,0],$(\frac{n-1}{n})^{2}+ln\frac{n+1}{n}$<1,即可证明结论.
解答 解:(Ⅰ)f′(x)=$\frac{2{x}^{2}-2ax+1}{x-a}$(x>a),∴f(x)有两个不同的极值点,
令h(x)=2x2-2ax+1,则h(x)有两个大于a的零点,(2分)
∴$\left\{\begin{array}{l}{△=4{a}^{2}-8>0}\\{h(a)>0}\\{a<\frac{a}{2}}\end{array}\right.$,∴a<-$\sqrt{2}$; (4分)
(Ⅱ)由(Ⅰ)知当a≤-2时,f(x)在(a,$\frac{a-\sqrt{{a}^{2}-2}}{2}$],[$\frac{a+\sqrt{{a}^{2}-2}}{2}$,+∞)上单调递增;
在($\frac{a-\sqrt{{a}^{2}-2}}{2}$,$\frac{a+\sqrt{{a}^{2}-2}}{2}$]上单调递减,($\frac{a-\sqrt{{a}^{2}-2}}{2}$<-1,$\frac{a+\sqrt{{a}^{2}-2}}{2}$<0,-------------------------(8分)
注意到h(x)=2x2-2ax+1的对称轴x=$\frac{a}{2}$<-1,h(-1)=3+2a<0,h(0)=1>0,可推知-1<x2<0,
∴当x∈[-1,0]时,g(a)=f(x)max=max{f(-1),f(0)}---------------------(9分)
而f(0)=ln(-a),f(-1)=1+ln(-1-a),
又若f(0)>f(-1),a=-$\frac{e}{e-1}$>-2,故f(0)>f(-1)不成立
综上分析可知,g(a)=f(-1)=1+ln(-1-a)(a≤-2)…(10分)
(Ⅲ)证明:由(2)知,当a=-2时,x2+ln(x+2)≤1
令x+2=$\frac{n+1}{n}$,则x=-$\frac{n-1}{n}$∈(-1,0],∴$(\frac{n-1}{n})^{2}+ln\frac{n+1}{n}$<1,
∴ln$\frac{n+1}{n}$<$\frac{2}{n}$-$\frac{1}{{n}^{2}}$,即$\frac{1}{{n}^{2}}$+ln$\frac{n+1}{n}$<$\frac{2}{n}$ (12分)
∴$\sum_{i=1}^{n}$$\frac{1}{i(i+2)}$+$\sum_{i=1}^{n}$ln$\frac{i+1}{i}$<$\sum_{i=1}^{n}$$\frac{1}{{i}^{2}}$+$\sum_{i=1}^{n}$ln$\frac{i+1}{i}$<$\sum_{i=1}^{n}$$\frac{2}{i}$
∴$\frac{3{n}^{2}+5n}{4{n}^{2}+12n+8}$+ln$\sqrt{n+1}$<$\sum_{i=1}^{n}$$\frac{2}{i}$,
∴$\frac{3{n}^{2}+5n}{8{n}^{2}+24n+16}$+ln$\sqrt{n+1}$$<1+\frac{1}{2}+\frac{1}{3}$+…+$\frac{1}{n}$,n∈N*. (14分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及二次函数的性质,是一道综合题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
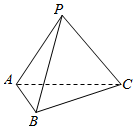 如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,且△PAC是等边三角形,AC=2,AB⊥BC,且AB=BC.过点B的平面α与直线PC平行,且与平面PAC垂直,设α与AC交于点O,与PA交于点D.
如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,且△PAC是等边三角形,AC=2,AB⊥BC,且AB=BC.过点B的平面α与直线PC平行,且与平面PAC垂直,设α与AC交于点O,与PA交于点D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,PB⊥底面ABCD,底面ABCD为直角梯形,∠ABC=90°,AD∥BC,∠BCD=45°,AB=AD=PB=1,点E在棱PA上,且PE=2EA.
如图,四棱锥P-ABCD中,PB⊥底面ABCD,底面ABCD为直角梯形,∠ABC=90°,AD∥BC,∠BCD=45°,AB=AD=PB=1,点E在棱PA上,且PE=2EA.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com