
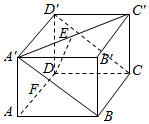
 如图所示,在长方体ABCD-A′B′C′D′中,AB=λAD=λAA′(λ>0),E,F分别是A′C′和AD的中点,且EF⊥平面A′BCD′.
如图所示,在长方体ABCD-A′B′C′D′中,AB=λAD=λAA′(λ>0),E,F分别是A′C′和AD的中点,且EF⊥平面A′BCD′.分析 (1)以D为原点,DA、DC、DD′分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出λ的值.
(2)求出平面EA′B的一个法向量和平面A′BC的法向量,利用向量法能求出二面角C-A′B-E的余弦值.
解答 解:(1)以D为原点,DA、DC、DD′分别为x,y,z轴,建立空间直角坐标系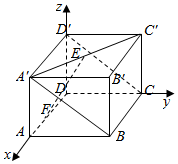
D(0,0,0),A′(2,0,2),D′(0,0,2),
B(2,2λ,0),C(0,2λ,0),
E(1,λ,2),F(1,0,0),$\overrightarrow{EF}$=(0,-λ,-2),
$\overrightarrow{{D}^{'}{A}^{'}}$=(2,0,0),$\overrightarrow{{A}^{'}B}$=(0,2λ,-2),
∵EF⊥平面A′BCD′,
∴EF⊥D′A′,EF⊥A′B,∴$\left\{\begin{array}{l}{\overrightarrow{EF}•\overrightarrow{{D}^{'}{A}^{1}}=0}\\{\overrightarrow{EF}•\overrightarrow{{A}^{'}B}=-2{λ}^{2}+4=0}\end{array}\right.$,
解得$λ=\sqrt{2}$或$λ=-\sqrt{2}$(舍),
∴λ的值为$\sqrt{2}$.
解:(2)设平面EA′B的一个法向量为$\overrightarrow{m}$=(1,y,z),则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{{A}^{'}B}=0}\\{\overrightarrow{m}•\overrightarrow{{A}^{'}E}=0}\end{array}\right.$,
∵$\overrightarrow{{A}^{'}B}=(0,2\sqrt{2},-2)$,$\overrightarrow{{A}^{'}E}$=(-1,$\sqrt{2}$,0),
∴$\left\{\begin{array}{l}{2\sqrt{2}y-2z=0}\\{-1+\sqrt{2}y=0}\end{array}\right.$,∴y=$\frac{\sqrt{2}}{2}$,z=1,∴$\overrightarrow{m}$=(1,$\frac{\sqrt{2}}{2}$,1),
∵EF⊥平面A′BCD′.
∴$\overrightarrow{EF}$=(0,-$\sqrt{2}$,-2)是平面A′BC的法向量,
∴cos<$\overrightarrow{m},\overrightarrow{EF}$>=$\frac{\overrightarrow{m}•\overrightarrow{EF}}{|\overrightarrow{m}|•|\overrightarrow{EF}|}$=$\frac{0-1-2}{\sqrt{\frac{5}{2}×\sqrt{6}}}$=-$\frac{\sqrt{15}}{5}$,
由图形知二面角C-A′B-E的平面角为锐角,
∴二面角C-A′B-E的余弦值为$\frac{\sqrt{15}}{5}$.
点评 本题考查实数值的求法,考查二面角的余弦值的求法,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,0] | B. | (-1,0) | C. | [0,+∞) | D. | [0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{{\sqrt{5}}}{5}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三菱柱ABC-A1B1C1中,平面A1C1CA和平面B1C1CB均为正方形,B1C1⊥A1C1,M为CC1的中点,B1C1=2,点D在线段AC上运动(不含端点A、C).
如图,在三菱柱ABC-A1B1C1中,平面A1C1CA和平面B1C1CB均为正方形,B1C1⊥A1C1,M为CC1的中点,B1C1=2,点D在线段AC上运动(不含端点A、C).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
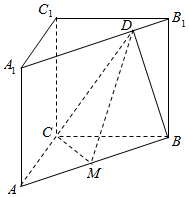 如图,直角三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=CC1,M为AB的中点,D在A1B1上且A1D=3DB1.
如图,直角三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=CC1,M为AB的中点,D在A1B1上且A1D=3DB1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com