
���� �Ѳ������̷ֱ�Ϊ��ͨ���̣��������̵õ�����x��һԪ���η��̣����ø���ϵ���Ĺ�ϵ���ҳ���ʽ���ɵó���
��� �⣺ֱ��l�IJ�������Ϊ$\left\{\begin{array}{l}{x=\frac{3}{2}+t}\\{y=\sqrt{3}t}\end{array}\right.$��tΪ����������Ϊ��ͨ���̣�2$\sqrt{3}x$-2y-3$\sqrt{3}$=0��
����C�IJ�������Ϊ$\left\{\begin{array}{l}{x=\frac{2}{3}{m}^{2}}\\{y=2m}\end{array}\right.$��mΪ����������Ϊ��ͨ���̣�y2=6x��
����$\left\{\begin{array}{l}{2\sqrt{3}x-2y-3\sqrt{3}=0}\\{{y}^{2}=6x}\end{array}\right.$������4x2-20x+9=0��
��x1+x2=5��x1x2=$\frac{9}{4}$��
��|AB|=$\sqrt{��1+3��[��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}]}$=$\sqrt{4����25-4��\frac{9}{4}��}$=8��
���� ���⿼���˲������̻�Ϊ��ͨ���̡�һԪ���η��̵ĸ���ϵ���Ĺ�ϵ���ҳ���ʽ��ֱ���������ཻ���⣬������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
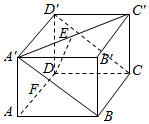 ��ͼ��ʾ���ڳ�����ABCD-A��B��C��D���У�AB=��AD=��AA�䣨�ˣ�0����E��F�ֱ���A��C���AD���е㣬��EF��ƽ��A��BCD�䣮
��ͼ��ʾ���ڳ�����ABCD-A��B��C��D���У�AB=��AD=��AA�䣨�ˣ�0����E��F�ֱ���A��C���AD���е㣬��EF��ƽ��A��BCD�䣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5$\sqrt{5}$ | B�� | 15 | C�� | 6$\sqrt{5}$ | D�� | 30 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��$\frac{1}{8}$��+�ޣ� | B�� | ��$\frac{1}{3}$��$\frac{{2\sqrt{2}}}{3}$�� | C�� | ��$\frac{{\sqrt{2}}}{4}$��+�ޣ� | D�� | ��2$\sqrt{2}$��3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
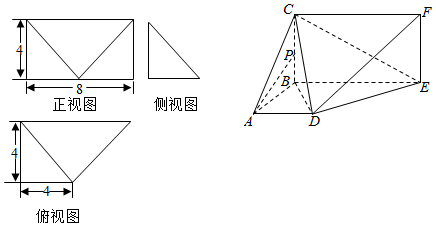
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com