
| A. | f(sinA)>f(cosB) | B. | f(cosB)>f(sinA) | C. | f(sinA)>f(sinB) | D. | f(cosB)>f(cosA) |
分析 由题意可得f(x)的图象关于直线x=2对称,且在[-1,0]递减,即有f(-x)=f(x),可得f(x)为偶函数,可得f(x)在[0,1]递增,由A,B是锐角三角形的两个内角,可得A+B>$\frac{π}{2}$,运用诱导公式和正弦函数的图象和性质,结合f(x)的单调性,即可得到结论.
解答 解:定义在R上的周期为2的函数,满足f(2+x)=f(2-x),在[-3,-2]上是减函数,
可得f(x)的图象关于直线x=2对称,且在[-1,0]递减,
由f(-x)=f(4+x),且f(x+4)=f(x),
即有f(-x)=f(x),可得f(x)为偶函数,
可得f(x)在[0,1]递增,
由A,B是锐角三角形的两个内角,可得A+B>$\frac{π}{2}$,
即$\frac{π}{2}$>A>$\frac{π}{2}$-B>0,
可得sinA>sin($\frac{π}{2}$-B)=cosB,
由sinA,cosB∈(0,1),
可得f(sinA)>f(cosB).
故选:A.
点评 本题考查函数的周期性和对称性、奇偶性的判断和运用,考查单调性的运用,以及正弦函数的图象和性质,考查运算能力,属于中档题.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{3}-{y^2}$=1 | B. | $\frac{y^2}{3}-{x^2}$=1 | C. | y2-$\frac{x^2}{3}$=1 | D. | $\frac{x^2}{2}-\frac{y^2}{2}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
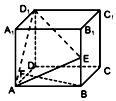 在如图所示的正四棱柱ABCD-A1B1C1D1中,E、F分别是棱B1B、AD的中点,直线BF与平面AD1E的位置关系是( )
在如图所示的正四棱柱ABCD-A1B1C1D1中,E、F分别是棱B1B、AD的中点,直线BF与平面AD1E的位置关系是( )| A. | 平行 | B. | 相交但不垂直 | C. | 垂直 | D. | 异面 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x>3是x>5的充分条件 | B. | x2=1是x=1的充分条件 | ||
| C. | a>b是ac2>bc2的必要条件 | D. | $α=\frac{π}{2}是sinα=1的必要条件$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-x2+1 | B. | y=x-2 | C. | y=log2x | D. | y=($\frac{1}{2}$)x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-∞,-\sqrt{2}})$ | B. | $({-∞,\sqrt{2}})$ | C. | $({-∞,2\sqrt{2}})$ | D. | $({-2\sqrt{2},\frac{{\sqrt{2}}}{2}})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com