
分析 ①根据椭圆短轴的定义进行判断.
②根据双曲线的性质进行判断.
③根据椭圆的定义进行判断.
④根据抛物线焦点的定义进行判断.
解答 解:①由椭圆$\frac{{x}^{2}}{2}$+y2=1得b=1,则短轴长为2b=2;故①错误,
②双曲线$\frac{{x}^{2}}{2}$-y2=1的焦点在x轴上;正确,
③设定点F1(0,-3)、F2(0,3),动点P(x,y)满足条件|PF1|+|PF2|=a(a>0),
当a>6时,则动点P的轨迹是椭圆;当a≤6时,轨迹不是椭圆,故③错误,
④抛物线y=8x2的标准方程为x2=$\frac{1}{8}$y,则焦点坐标是(0,$\frac{1}{32}$).故④错误,
故答案为:②.
点评 本题主要考查命题的真假判断,涉及双曲线,抛物线和椭圆的性质,比较基础.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
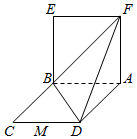 已知四边形ABCD为平行四边形,BD⊥AD,BD=AD,AB=2,四边形ABEF为正方形,且平面ABEF⊥平面ABCD.
已知四边形ABCD为平行四边形,BD⊥AD,BD=AD,AB=2,四边形ABEF为正方形,且平面ABEF⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{3}$ | C. | 3 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{4\sqrt{5}}}{5}$ | B. | $\frac{{8\sqrt{5}}}{5}$ | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com