
分析 (1)求出函数的导数,根据切线方程求出a的值,求出A的坐标,得到关于b的方程,解出即可;
(2)设出切点A,根据切线方程求出A的坐标,从而求出切线方程,整理即可;
(3)问题转化为x∈(-∞,2]时,f(x)≤$\frac{3}{4}$x+$\frac{9}{8}$,令k(x)=$\frac{3}{4}$x+$\frac{9}{8}$-f(x)=-x3+x2+$\frac{7}{4}$x+$\frac{1}{2}$,根据函数的单调性证明即可.
解答 解:(1)f′(x)=3ax2-2x-1,
∵f(x)的图象在x=-$\frac{1}{2}$处的切线方程是y=$\frac{3}{4}$x+$\frac{9}{8}$,
故f′(-$\frac{1}{2}$)=$\frac{3}{4}$,即3a•(-$\frac{1}{2}$)2•(-$\frac{1}{2}$)-1=$\frac{3}{4}$,解得:a=1;
故f(x)的图象过A(-$\frac{1}{2}$,$\frac{3}{4}$),
故(-$\frac{1}{2}$)3-(-$\frac{1}{2}$)2-(-$\frac{1}{2}$)+b=$\frac{3}{4}$,解得:b=$\frac{5}{8}$,
综上,a=1,b=$\frac{5}{8}$;
(2)设直线y=$\frac{3}{4}$x+$\frac{9}{8}$与函数g(x)的图象相切于A(x0,y0),
∵g′(x)=$\frac{3\sqrt{e}}{4}$ex,∴过A点的直线的斜率是g′(x0)=$\frac{3\sqrt{e}}{4}$e${\;}^{{x}_{0}}$,
又直线y=$\frac{3}{4}$x+$\frac{9}{8}$的斜率是$\frac{3}{4}$,
故$\frac{3\sqrt{e}}{4}$e${\;}^{{x}_{0}}$=$\frac{3}{4}$,解得:x0=-$\frac{1}{2}$,
将x0=-$\frac{1}{2}$代入y=$\frac{3\sqrt{e}}{4}$ex,得点A的坐标是(-$\frac{1}{2}$,$\frac{3}{4}$),
故切线方程为:y-$\frac{3}{4}$=$\frac{3}{4}$(x+$\frac{1}{2}$),化简得y=$\frac{3}{4}$x+$\frac{9}{8}$,
故直线y=$\frac{3}{4}$x+$\frac{9}{8}$可以与函数g(x)的图象相切,切点坐标是(-$\frac{1}{2}$,$\frac{3}{4}$);
(3)证明:要证明:x∈(-∞,2]时,f(x)≤g(x),
只需证明x∈(-∞,2]时,f(x)≤$\frac{3}{4}$x+$\frac{9}{8}$,
令k(x)=$\frac{3}{4}$x+$\frac{9}{8}$-f(x)=-x3+x2+$\frac{7}{4}$x+$\frac{1}{2}$,
k′(x)=-3x2+2x+$\frac{7}{4}$,令k′(x)=-3x2+2x+$\frac{7}{4}$=0,
解得:x=-$\frac{1}{2}$,x=$\frac{7}{6}$,
故k(x)min=min{k(-$\frac{1}{2}$),k(2)},
∵k(-$\frac{1}{2}$)=0,k(2)=0,故k(x)min=0,
故?x∈(-∞,2],f(x)≤$\frac{3}{4}$x+$\frac{9}{8}$成立,
?x∈(-∞,2],令h(x)=g(x)-($\frac{3}{4}$x+$\frac{9}{8}$)=$\frac{3\sqrt{e}}{4}$ex-$\frac{3}{4}$x-$\frac{9}{8}$,
h′(x)=$\frac{3\sqrt{e}}{4}$ex-$\frac{3}{4}$,令h′(x)=0,x=-$\frac{1}{2}$,
x∈(-∞,-$\frac{1}{2}$)时,h′(x)<0,当x∈(-$\frac{1}{2}$,2]时,h′(x)>0,
故h(x)≥h(-$\frac{1}{2}$)=0,即?x∈(-∞,2]时,g(x)≥$\frac{3}{4}$x+$\frac{9}{8}$,
由不等式的性质的传递性得:x∈(-∞,2]时,f(x)≤g(x).
点评 本题考查了切线方程问题,考查导数的应用以及不等式的证明,是一道综合题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
| 天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 空气质量指数 | 7.1 | 8.3 | 7.3 | 9.5 | 8.6 | 7.7 | 8.7 | 8.8 | 8.7 | 9.1 |
| 天数 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 空气质量指数 | 7.4 | 8.5 | 9.7 | 8.4 | 9.6 | 7.6 | 9.4 | 8.9 | 8.3 | 9.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
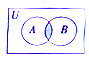
| A. | {1,2,3,4,5} | B. | {3,4,5,6,7} | C. | {1,2,3,4,5,6,7} | D. | {3,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $0<\frac{b}{a}≤\frac{3}{2}$ | B. | $\frac{b}{a}≥\frac{3}{2}$ | C. | $0<\frac{b}{a}≤\frac{{\sqrt{5}}}{2}$ | D. | $\frac{b}{a}≥\frac{{\sqrt{5}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com