
分析 (1)设数列{an}的公差为d(d≠0),由a1,a2,a5成等比数列列式求得d,则等差数列的通项公式可求;设数列{bn}的首项为b1,由${S_3}=\frac{13}{3}$,q=3,可得关于b1的方程,求得b1,则等比数列的通项公式可求;
(2)把数列{an},{bn}的通项公式代入cn=an•bn,利用错误相减法求数列{cn}的前项和Tn.
解答 解:(1)设数列{an}的公差为d(d≠0),
由a1,a2,a5成等比数列,得(1+d)2=1×(1+4d),
即d2=2d,解得d=2.
∴an=1+2(n-1)=2n-1.
设数列{bn}的首项为b1,由${S_3}=\frac{13}{3}$,q=3,
得${b}_{1}+3{b}_{1}+9{b}_{1}=13{b}_{1}=\frac{13}{3}$,∴b1=3.
则${b}_{n}={3}^{n}$;
(2)cn=an•bn=(2n-1)•3n,
∴${T}_{n}=1•{3}^{1}+3•{3}^{2}+…+(2n-3)•{3}^{n-1}+(2n-1)•{3}^{n}$,
则$3{T}_{n}=1•{3}^{2}+3•{3}^{3}+…+(2n-3)•{3}^{n}+(2n-1)•{3}^{n+1}$,
两式作差可得:$-2{T}_{n}=3+2({3}^{2}+{3}^{3}+…+{3}^{n})-(2n-1)•{3}^{n+1}$
=3+2$•\frac{9(1-{3}^{n-1})}{1-3}-(2n-1)•{3}^{n+1}$,
则${T}_{n}=(n-1)•{3}^{n}+1$.
点评 本题考查等差数列与等比数列的通项公式,训练了错位相减法求数列的前n项和,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | f(2)<f(-2)<f(0) | B. | f(0)<f(2)<f(-2) | C. | f(-2)<f(0)<f(2) | D. | f(-)<f(-2)<f(2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 0 | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
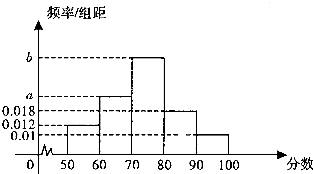
| A. | 0.024 | B. | 0.036 | C. | 0.06 | D. | 0.6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2+\sqrt{3}$ | B. | $-2-\sqrt{3}$ | C. | $2-\sqrt{3}$ | D. | $-2+\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的上、下顶点分别为A,B,右焦点为F,点$P(\frac{{2\sqrt{13}}}{13},\frac{{2\sqrt{39}}}{13})$在椭圆C上,且OP⊥AF.
椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的上、下顶点分别为A,B,右焦点为F,点$P(\frac{{2\sqrt{13}}}{13},\frac{{2\sqrt{39}}}{13})$在椭圆C上,且OP⊥AF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 必要不充分 | B. | 充分不必要 | ||
| C. | 充分必要 | D. | 既不充分也不必要 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com