
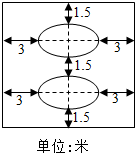
 ijѧУ���ڹ㳡�Ͻ���һ�����λ�����ͼ��ʾ���м�����ȫ��ͬ��������Բ�ͻ�̳��ÿ����Բ�ͻ�̳�������Ϊ216��ƽ���ף�������Բ��̳�ľ�����1.5�ף��������λ�̳��ռ�����ΪS��
ijѧУ���ڹ㳡�Ͻ���һ�����λ�����ͼ��ʾ���м�����ȫ��ͬ��������Բ�ͻ�̳��ÿ����Բ�ͻ�̳�������Ϊ216��ƽ���ף�������Բ��̳�ľ�����1.5�ף��������λ�̳��ռ�����ΪS������ ��1������ͼ���������ݣ�������ã�S=��2a+6����4b+$\frac{9}{2}$����
��2�����æ�ab=216�У��ɵ�ab=216�������û�������ʽ���ɵó����ۣ�
���  �⣺��1��������ã�S=��2a+6����4b+$\frac{9}{2}$��=8ab+9a+24b+27����5�֣�
�⣺��1��������ã�S=��2a+6����4b+$\frac{9}{2}$��=8ab+9a+24b+27����5�֣�
��2���ߦ�ab=216�У���ab=216
��S=8ab+9a+24b+27��8��216+27+2$\sqrt{9a•24b}$=2187
���ҽ���9a=24b����a=24ʱ��ȡ��=������ʱ2a=48 ����12�֣�
�𣺵���Բ�λ�̳�ij���Ϊ48��ʱ���������λ�ռ�����٣�ռ�����Ϊ2187ƽ����..��..��13�֣�
���� ������Ҫ���麯����ʵ�������е�Ӧ���Լ����ö�Ԫ����ʽ����ֵ�ķ��������ʵ������ͨ�����ĸ����裺��1���Ķ����⣬�������⣻��2��������ѧ���ţ�������ѧģ�ͣ���3��������ѧ�ķ������õ���ѧ�������4��ת��ɾ�����������������йؼ��ǽ�����ѧģ�ͣ�


 ͬ����ϰǿ����չϵ�д�
ͬ����ϰǿ����չϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 18 | B�� | 26 | C�� | 28 | D�� | 36 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��$\frac{1}{2}$��+�ޣ� | B�� | ��-2��-$\frac{1}{2}$�� | C�� | ��-�ޣ�-$\frac{1}{2}$�� | D�� | ��-�ޣ�-2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��������ƽ�У�������涼��ƽ���ı��εļ���������� | |
| B�� | ��һ�����Ƕ���Σ�������涼�������εļ�������� | |
| C�� | �������Χ�ɵĶ�����һ�������� | |
| D�� | ��̨��������ӳ��߽���һ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-1��1�� | B�� | ��-1��0���ȣ�1��+�ޣ� | C�� | ��-�ޣ�-1���ȣ�1��+�ޣ� | D�� | ��-�ޣ�-1���ȣ�0��1�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com