
分析 (1)法一:写出曲线与坐标轴的交点坐标,利用圆心的几何特征设出圆心坐标,构造关于圆心坐标的方程,通过解方程确定出圆心坐标,进而算出半径,写出圆的方程;
法二:可设出圆的一般式方程,利用曲线与方程的对应关系,根据同一性直接求出参数,
(2)利用点斜式设出直线方程,根据直线被圆截得的弦长为$4\sqrt{2}$求解k,可得直线方程.
(3)利用设而不求思想设出圆C与直线x-y+a=0的交点A,B坐标,通过OA⊥OB建立坐标之间的关系,结合韦达定理寻找关于a的方程,通过解方程确定出a的值.
解答 解:(1)法一:曲线y=x2-6x+1与y轴的交点为(0,1),与x轴的交点为(3+2$\sqrt{2}$,0),(3-2$\sqrt{2}$,0).
可知圆心在直线x=3上,故可设该圆的圆心C为(3,t),则有32+(t-1)2=(2$\sqrt{2}$)2+t2,解得t=1,
故圆C的半径为 $\sqrt{9{+(t-1)}^{2}}$=3,所以圆C的方程为(x-3)2+(y-1)2=9.
法二:设圆的方程为x2+y2+Dx+Ey+F=0,
圆过(0,1)即x=0,y=1有1+E+F=0,
y=0,x2 -6x+1=0与x2+Dx+F=0是同一方程,故有D=-6,F=1,E=-2,
即圆方程为x2+y2-6x-2y+1=0.
(2)直线过定点(2,3),当k存在时,设直线方程为y-3=k(x-2),即kx-y+3-2k=0.
由(1)可知圆心为(3,1),半径r=3.
圆心到直线的距离d=$\frac{|3k-1+3-2k|}{\sqrt{{k}^{2}+1}}$,
由直线被圆截得的弦长公式l=4$\sqrt{2}$=2$\sqrt{{r}^{2}-{d}^{2}}$,
解得:k=$-\frac{3}{4}$.
∴直线方程为3x+4y-18=0.
当k不存在时,设直线方程为x=2,圆心为(3,1),半径r=3.
圆心到直线的距离d=1,
直线被圆截得的弦长公式l=2$\sqrt{{r}^{2}-{d}^{2}}$=4$\sqrt{2}$,满足题意,
故得过定点(2,3)与圆相交所截得的弦长为$4\sqrt{2}$的直线方程为x=2或3x+4y-18=0.
(3)设A(x1,y1),B(x2,y2),
其坐标满足方程组$\left\{\begin{array}{l}{x-y+a=0}\\{{(x-3)}^{2}{+(y-1)}^{2}=9}\end{array}\right.$,
消去y,得到方程2x2+(2a-8)x+a2-2a+1=0,
由已知可得判别式△=56-16a-4a2>0.
在此条件下利用根与系数的关系得到x1+x2=4-a,x1x2=$\frac{{a}^{2}-2a+1}{2}$①,
由于OA⊥OB可得x1x2+y1y2=0,又y1=x1+a,y2=x2+a,
所以可得2x1x2+a(x1+x2)+a2=0②
由①②可得a=-1,满足△=56-16a-4a2>0;
故a=-1.
点评 本题考查圆的方程的求解,考查学生的待定系数法,考查学生的方程思想,直线与圆的相交问题的解决方法和设而不求的思想,考查垂直问题的解决思想,考查学生分析问题解决问题的能力,属于直线与圆的方程的基本题型.


科目:高中数学 来源: 题型:选择题
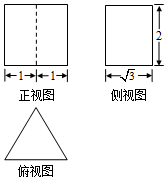
| A. | $\frac{4}{3}π$ | B. | $\frac{{32\sqrt{3}}}{27}π$ | C. | $\frac{{28\sqrt{3}}}{27}π$ | D. | $\frac{{28\sqrt{21}}}{27}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{7}{3}$ | C. | $\frac{13}{4}$ | D. | $\frac{43}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{1}{2}\sqrt{3}$ | D. | $\frac{1}{4}\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com