
 Ϊ���С��¿��á���ѧ����ij��ѧ��ʦ�ֱ���ԭ��ͳ��ѧ�͡��¿��á����ֲ�ͬ�Ľ�ѧ��ʽ���ڼס�������ƽ�а���н�ѧʵ�飬Ϊ�˽��ѧЧ�������п��Ժֱ�������༶�и������ȡ20��ѧ���ijɼ�����ͳ�ƣ������ľ�Ҷͼ��ͼ���dzɼ�������70����Ϊ���ɼ���������
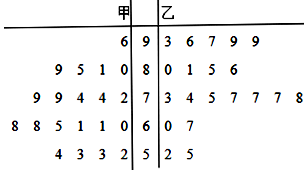
Ϊ���С��¿��á���ѧ����ij��ѧ��ʦ�ֱ���ԭ��ͳ��ѧ�͡��¿��á����ֲ�ͬ�Ľ�ѧ��ʽ���ڼס�������ƽ�а���н�ѧʵ�飬Ϊ�˽��ѧЧ�������п��Ժֱ�������༶�и������ȡ20��ѧ���ijɼ�����ͳ�ƣ������ľ�Ҷͼ��ͼ���dzɼ�������70����Ϊ���ɼ���������| �װ� | �Ұ� | �ܼ� | |
| �ɼ����� | |||
| �ɼ������� | |||
| �ܼ� |
| P��K2��0�� | 0.10 | 0.05 | 0.025 | 0.010 |
| K0 | 2.706 | 3.841 | 5.024 | 6.635 |
���� ��1�����ݾ�Ҷͼ����ס���������ѧ�ɼ�ǰ10��ѧ����ƽ���ּ��ɣ�
��2����д������������K2�������������ɵó����ۣ�
��� �⣺��1����ƽ����$\frac{1}{10}$����96+80+81+85+89+72+74+74+79+79��=80.9���ҵ�ƽ����$\frac{1}{10}$����93+96+97+99+99+80+81+85+86+78��=89.4 ����6�֣�
��2��
| �װ� | �Ұ� | �ܼ� | |
| �ɼ����� | 10 | 16 | 26 |
| �ɼ������� | 10 | 4 | 14 |
| �ܼ� | 20 | 20 | 40 |
���� ���⿼���˼���ƽ����������Լ����Ӧ�����⣬����ʱӦ��������������۲�ֵ�������ٽ�ֵ���ó����ۣ��ǻ�����Ŀ��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪����A-BPC�У�AP��PC��AC��BC��MΪAB���е㣬DΪPB���е㣬�ҡ�PMBΪ�������Σ�
��ͼ����֪����A-BPC�У�AP��PC��AC��BC��MΪAB���е㣬DΪPB���е㣬�ҡ�PMBΪ�������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
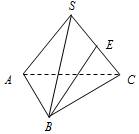 ��ͼ������S-ABC�У���$AC=2\sqrt{3}$��SA=SB=SC=AB=BC=4��EΪ��SC���е㣬��ֱ��AC��BE���ɽǵ�����ֵΪ$\frac{1}{4}$��ֱ��AC��ƽ��SAB���ɵĽ�Ϊ600��
��ͼ������S-ABC�У���$AC=2\sqrt{3}$��SA=SB=SC=AB=BC=4��EΪ��SC���е㣬��ֱ��AC��BE���ɽǵ�����ֵΪ$\frac{1}{4}$��ֱ��AC��ƽ��SAB���ɵĽ�Ϊ600���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{5}$ | B�� | $2\sqrt{5}$ | C�� | $3\sqrt{5}$ | D�� | $4\sqrt{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3}{2}$ | B�� | $\frac{2}{3}$ | C�� | -$\frac{3}{2}$ | D�� | -$\frac{2}{3}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com