
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的最大值即可;
(2)问题等价于求函数F(x)=h(x)-g(x)的零点个数,通过讨论a的范围判断即可.
解答 解:(1)$f'(x)=\frac{-lnx}{x^2}$,由f'(x)=0⇒x=1,列表如下:
| x | (0,1) | 1 | (1,+∞) |
| f'(x) | + | 0 | - |
| f(x) | 单调递增 | 极大值1 | 单调递减 |
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,考查函数的零点问题,是一道综合题.


科目:高中数学 来源: 题型:选择题
| A. | $({\frac{3}{2},\sqrt{3}})$ | B. | $({\frac{{\sqrt{3}}}{2},\frac{3}{2}})$ | C. | $({\frac{3}{2},\sqrt{3}}]$ | D. | $({\frac{{\sqrt{3}}}{2},\sqrt{3}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{10}$x±2y=0 | B. | 2x±$\sqrt{10}$y=0 | C. | $\sqrt{6}$x±2y=0 | D. | 2x±$\sqrt{6}$y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | α∩γ=m,α⊥γ,β⊥γ | B. | α⊥β,β⊥γ,m⊥α | C. | α⊥β,α∩β=n,m⊥n | D. | n⊥α,n⊥β,m⊥α |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,$\sqrt{2}$] | B. | ($\frac{\sqrt{2}}{2}$,1) | C. | ($\frac{\sqrt{2}}{2}$,$\sqrt{2}$) | D. | (1,$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{\sqrt{3}-1}{2}$ | C. | $\frac{\sqrt{5}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
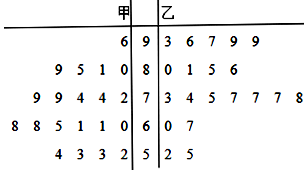 为推行“新课堂”教学法,某数学老师分别用原传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班进行教学实验,为了解教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出的茎叶图如图.记成绩不低于70分者为“成绩优良”.
为推行“新课堂”教学法,某数学老师分别用原传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班进行教学实验,为了解教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出的茎叶图如图.记成绩不低于70分者为“成绩优良”.| 甲班 | 乙班 | 总计 | |
| 成绩优良 | |||
| 成绩不优良 | |||
| 总计 |
| P(K2≥0) | 0.10 | 0.05 | 0.025 | 0.010 |
| K0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com