练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    函数f(x)＝3ax＋1－2a在(－1,1)上存在x0，使f(x0)＝0，则a的取值范围是(　　)

    A．－1<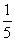a<                                                B．a>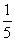

    C．a<－1或a>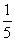                                         D．a<－1


    C

    [分析]　a≠0时，f(x)为一次函数，故由x0∈(－1,1)时，f(x0)＝0知，f(－1)与f(1)异号．

    [解析]　由题意得f(－1)·f(1)<0，

    即(－3a＋1－2a)·(3a＋1－2a)<0，

    即(5a－1)(a＋1)>0，∴a<－1或a>.故选C.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    在△ABC中，a，b，c分别是内角A，B，C的对边，且cos2B＋3cos(A＋C)＋2＝0，b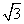＝，则c:sinC等于(　　)

    A．3:1                                                           B.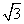:1

    C.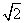:1                                                         D．2;1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设m>1，在约束条件下，目标函数z＝x＋5y的最大值为4，则m的值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知x＋3y－2＝0，则3x＋27y＋1的最小值是(　　)

    A．3                                                       B．1＋2

    C．6                                                             D．7

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    围建一个面积为360m2的矩形场地，要求矩形场地的一面利用旧墙(利用旧墙需维修)，其他三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2m的进出口，如图所示，已知旧墙的维修费用为45元/m，新墙的造价为180元/m，设利用的旧墙的长度为x(x>0)(单位：元)．

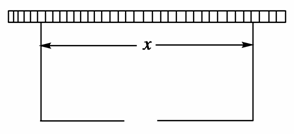
    (1)将总费用y表示为x的函数；

    (2)试确定x，使修建此矩形场地围墙的总费用最小，并求最小总费用．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    关于x的不等式＜1的解集为{x|x＜1或x＞2}，则实数a＝____________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)＝ax3＋bx2＋cx在区间[0,1]上是增函数，在区间(－∞，0)，(1，＋∞)上是减函数．又f ′＝.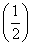

    (1)求f(x)的解析式；

    (2)若在区间[0，m](m>0)上恒有f(x)≤x成立，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    比较大小：lg9·lg11________1(填“>”“<”或“＝”)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知关于x的不等式x2-4x-m＜0的解集为非空集{x|n＜x＜5}
    （1）求实数m和n的值
    （2）求关于x的不等式loga（-nx2+3x+2-m）＞0的解集．

    查看答案和解析>>

    同步练习册答案