Question

9．如图所示，M，N是函数y=2sin（ωx+φ）（ω＞0）的图象与x轴的交点，点P在M，N之间的图象上运动，当△MPN面积最大时$\overrightarrow{PM}•\overrightarrow{PN}=0$，则实数ω等于$\frac{π}{4}$．

Answer 1

分析 根据向量$\overrightarrow{PM}•\overrightarrow{PN}$=$|\overrightarrow{PM}|•|\overrightarrow{PN}|•cosθ$=0，可知∠MPN=90°，过P点x轴的垂直交于Q，则QN=2，那么周期T=4QN=8，从而得到实数ω的值．

解答 解：由题意：∵向量$\overrightarrow{PM}•\overrightarrow{PN}$=$|\overrightarrow{PM}|•|\overrightarrow{PN}|•cosθ$；（0≤θ＜π
当△MPN面积最大时，P点到x的值最大，则P点在顶点，且有PN=PM．
∵$\overrightarrow{PM}•\overrightarrow{PN}=0$，
∴∠MPN=90°，即PN⊥PM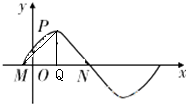
过P点x轴的垂直交于Q，
则QN=2，
那么：周期T=4QN=8，
∵周期T=8=$\frac{2π}{ω}$．
解得：$ω=\frac{π}{4}$．
故答案为：$\frac{π}{4}$．

点评 本题主要考查利用y=Asin（ωx+φ）的图象特征，由函数y=Asin（ωx+φ）的部分图象求解析式，属于中档题．