
| A. | [-1,1] | B. | [1,+∞) | C. | [2,+∞) | D. | (-∞,-2]∪[2,+∞) |
分析 利用构造法g(x)=f(x)-$\frac{1}{2}$x2,推出g(x)为奇函数,判断g(x)的单调性,然后推出不等式得到结果
解答 解:∵f(-x)+f(x)=x2,∴f(x)-x2+f(-x)=0,
令g(x)=f(x)-$\frac{1}{2}$x2,
则g(-x)+g(x)=f(-x)-$\frac{1}{2}$x2+f(x)-$\frac{1}{2}$x2=0
∴函数g(x)为奇函数.
∵x∈(0,+∞)时,g′(x)=f′(x)-x<0,
故函数g(x)在(0,+∞)上是减函数,
故函数g(x)在(-∞,0)上也是减函数,
由f(0)=0,可得g(x)在R上是减函数.
f(2-m)+f(-m)+2m-2≥0等价于f(2-m)-$\frac{1}{2}$(2-m)2≥f(m)-$\frac{1}{2}$ m2,
即g(2-m)≤g(m),
∴2-m≤m,解得m≥1
故选:B
点评 本题考查的知识点是全称命题,利用导数研究函数的单调性,难度中档.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,M,N是函数y=2sin(ωx+φ)(ω>0)的图象与x轴的交点,点P在M,N之间的图象上运动,当△MPN面积最大时$\overrightarrow{PM}•\overrightarrow{PN}=0$,则实数ω等于$\frac{π}{4}$.
如图所示,M,N是函数y=2sin(ωx+φ)(ω>0)的图象与x轴的交点,点P在M,N之间的图象上运动,当△MPN面积最大时$\overrightarrow{PM}•\overrightarrow{PN}=0$,则实数ω等于$\frac{π}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
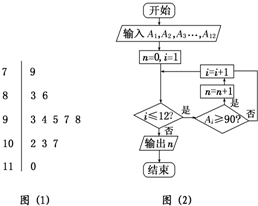 图(1)是某高三学生进入高中三年来的数学考试成绩的茎叶图,第1次到第12次的考试成绩依次记为A1,A2,…,A12.图(2)是统计茎叶图中成绩在一定范围内考试次数的一个程序框图.那么输出的结果是9.
图(1)是某高三学生进入高中三年来的数学考试成绩的茎叶图,第1次到第12次的考试成绩依次记为A1,A2,…,A12.图(2)是统计茎叶图中成绩在一定范围内考试次数的一个程序框图.那么输出的结果是9.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com