练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．f（x）=x2+（m-1）x+1在（0，2）与（2，4）各有1个零点，则m的取值范围是$（-\frac{13}{4}，-\frac{3}{2}）$．

    分析 由于f（x）=x2+（m-1）x+1在（0，2）与（2，4）各有1个零点，利用二次函数的性质和函数零点的存在定理列出不等式组，解得即可．

    解答 解：∵f（x）=x2+（m-1）x+1在（0，2）与（2，4）各有1个零点，
    ∴$\left\{\begin{array}{l}f（0）＞0\\ f（2）＜0\\ f（4）＞0\end{array}\right.$，即：$\left\{\begin{array}{l}1＞0\\ 2m+3＜0\\ 4m+13＞0\end{array}\right.$解得．$-\frac{13}{4}＜m＜-\frac{3}{2}$．
    则m的取值范围是：$（-\frac{13}{4}，-\frac{3}{2}）$．
    故答案为：$（-\frac{13}{4}，-\frac{3}{2}）$

    点评 本题考查了二次函数的性质和函数零点的存在定理等基础知识与基本方法，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    20．在等差数列{an}中，a1+a4+a7=15，a2+a5+a8=20，则a3+a6+a9=25．

    查看答案和解析>>

    科目：高中数学 来源：2017届湖北襄阳四中高三七月周考三数学（文）试卷（解析版） 题型：解答题

    选修4-5：不等式选讲

    已知函数．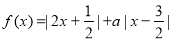

    （1）当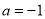时，解不等式；

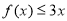    （2）当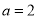时，若关于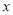的不等式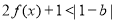的解集为空集，求实数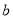的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

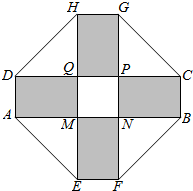    15．2010年上海世博会某国要建一座八边形的展馆区，它的主体造型的平面图是由两个相同的矩形ABCD和EFGH构成的面积为200m2的十字型地域，计划在正方形MNPQ上建一座“观景花坛”，造价为4200元/m2，在四个相同的矩形上（图中阴影部分）铺花岗岩地坪，造价为210元/m2，再在四个空角（如△DQH等）上铺草坪，造价为80元/m2．设AD长为xm，DQ长为ym．
    （1）试找出x与y满足的等量关系式；
    （2）设总造价为S元，试建立S与x的函数关系；
    （3）若总造价S不超过138000元，求AD长x的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

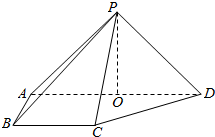    2．如图，在四棱锥P-ABCD中，侧面PAD⊥底面ABCD，侧棱PA=PD=$\sqrt{2}$，底面ABCD为直角梯形，其中BC∥AD，AB⊥AD，AD=2AB=2BC=2，O为AD中点．
    （Ⅰ）求证：PO⊥平面ABCD；
    （Ⅱ）求这个四棱锥的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知函数f（x）=xlnx．
    （I）记函数g（x）=$\frac{a{x}^{2}}{2}$，若?x0∈[1，e]使f（x0）＜g（x0）成立，求实数a的取值范围；
    （Ⅱ）记函数h（x）=（k-3）x-k+2，若x＞1时f（x）＞h（x）恒成立，求整数k的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知数列{an}的前n项和为Sn，且满足：①an＞0，②a1=2，③对任意n∈N+有$a_{n+1}^2-{a_n}{a_{n+1}}-2a_n^2=0$
    （1）求an及Sn；
    （2）已知数列{bn}的前n项和为Tn，若${b_n}+{b_{n+1}}=（{sin^2}\frac{nπ}{2}-{cos^2}\frac{nπ}{2}）•{log_2}{a_n}$；求T2016的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．定义在非零实数集上的函数f（x）满足：f（xy）=f（x）+f（y），且f（x）在区间（0，+∞）上为递增函数．
    （1）求f（1）、f（-1）的值；
    （2）求证：f（x）是偶函数；
    （3）解不等式$f（2）+f（x-\frac{1}{2}）≤0$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．如图，在△ABC中，AB=c，BC=a，CA=b．其中a=14，BC边上的高为12，内切圆半径r=4．求AB的长．

    查看答案和解析>>

    同步练习册答案