
分析 (1)利用赋值法即可求f(1)、f(-1)的值;
(2)根据函数奇偶性的定义即可证明f(x)是偶函数;
(3)根据函数奇偶性,利用数形结合即可解不等式$f(2)+f(x-\frac{1}{2})≤0$.
解答 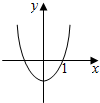 解:(1)令x=y=1,则f(1)=f(1)+f(1),
解:(1)令x=y=1,则f(1)=f(1)+f(1),
∴f(1)=0…(2分)
令x=y=-1,则f(1)=f(-1)+f(-1),
∴f(-1)=0…(4分)
(2)令y=-1,则f(-x)=f(x)+f(-1)=f(x),…(6分)
∴f(-x)=f(x)…(7分)
∴f(x)是偶函数 …(8分)
(3)根据题意可知,函数y=f(x)的图象大致如右图:
∵$f(2)+f(x-\frac{1}{2})=f(2x-1)≤0$,…(9分)
∴-1≤2x-1<0或0<2x-1≤1,…(11分)
∴$0≤x<\frac{1}{2}$或$\frac{1}{2}<x≤1$…(12分)
点评 本题主要考查抽象函数的应用以及函数奇偶性的判断,利用赋值法是解决本题的关键.


 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | [$\sqrt{2}$,3] | B. | [3,+∞) | C. | (0,$\frac{1}{3}$] | D. | [$\frac{1}{3}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
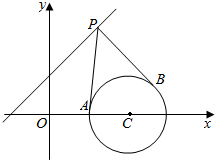 已知直线x-y+2=0和圆C:x2+y2-8x+12=0,过直线上的一点P(x0,y0)作两条直线PA,PB与圆C相切于A,B两点.①当P点坐标为(2,4)时,求以PC为直径的圆的方程,并求直线AB的方程;
已知直线x-y+2=0和圆C:x2+y2-8x+12=0,过直线上的一点P(x0,y0)作两条直线PA,PB与圆C相切于A,B两点.①当P点坐标为(2,4)时,求以PC为直径的圆的方程,并求直线AB的方程;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com