
分析 (1)当k=3时,f(x)=x2+3x的图象是开口朝上,且以直线x=-$\frac{3}{2}$为对称轴的抛物线,进而得到函数的最值和单调区间;
(2)若函数f(x)在[1,+∞)为增函数,则-$\frac{k}{2}$≤1,解得k的取值范围;
(3)分类讨论给定区间与对称轴的关系,进而分析函数的单调性,可得不同情况下函数的最小值.
解答 解:(1)当k=3时,f(x)=x2+3x的图象是开口朝上,且以直线x=-$\frac{3}{2}$为对称轴的抛物线,
故当x=-$\frac{3}{2}$时,函数取最小值为$-\frac{9}{4}$,…(2分)
函数f(x)=x2+3x的单调递增区间:$(-\frac{3}{2},+∞)$,…(4分)
函数f(x)=x2+3x的单调递减区间:$(-∞,-\frac{3}{2})$…(6分)
(2)函数f(x)=x2+kx+3-k的图象是开口朝上,且以直线x=-$\frac{k}{2}$为对称轴的抛物线,
若函数f(x)在[1,+∞)为增函数,
则-$\frac{k}{2}$≤1,
解得:k≥-2…(10分)
(3)函数f(x)=x2+kx+3-k的图象是开口朝上,且以直线x=-$\frac{k}{2}$为对称轴的抛物线,
当-$\frac{k}{2}$>2,即k<-4时,函数f(x)=x2+kx+3-k在[-2,2]上为减函数,当x=2时,函数f(x)的最小值为7+k;
当-2≤-$\frac{k}{2}$≤2,即-4≤k≤4时,函数f(x)=x2+kx+3-k在[-2,-$\frac{k}{2}$]上为减函数,在[-$\frac{k}{2}$,2]上为增函数,当x=-$\frac{k}{2}$时,函数f(x)的最小值为$-\frac{{k}^{2}}{4}-k+3$
当-$\frac{k}{2}$<-2,即k>4时,函数f(x)=x2+kx+3-k在[-2,2]上为增函数,当x=-2时,函数f(x)的最小值为7-3k;
综上所述函数f(x)的最小值为$\left\{\begin{array}{l}7+k,k<-4\\-\frac{{k}^{2}}{4}-k+3,-4≤k≤4\\ 7-3k,k>4\end{array}\right.$.…(14分)
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
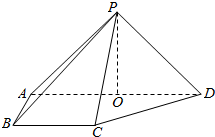 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届湖北襄阳四中高三七月周考三数学(文)试卷(解析版) 题型:解答题
选修4-4:坐标系与参数方程
已知曲线C的极坐标方程是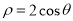 ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是
,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是 (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程和直线L的普通方程;
(2)设点P(m,0),若直线L与曲线C交于两点A,B,且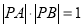 ,求实数m的值.
,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 级数 | 全月应纳税所得额 | 税率(%) |
| 1 | 不超过500元 | 5 |
| 2 | 500~2000元 | 10 |
| 3 | 2000~5000元 | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{5π}{6}$,$\frac{11π}{6}$] | B. | [$\frac{2π}{3}$,$\frac{5π}{3}$] | C. | [$\frac{π}{2}$,$\frac{3π}{2}$] | D. | [-$\frac{π}{2}$,0] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com