
| 级数 | 全月应纳税所得额 | 税率(%) |
| 1 | 不超过500元 | 5 |
| 2 | 500~2000元 | 10 |
| 3 | 2000~5000元 | 15 |
分析 法一、由题意求出按原税缴纳个人所得税123元的收入,然后计算按新税法所交的税款得答案;
法二、由题意建立按原税缴纳个人所得税的数学模型,算出个人收入,再按新税法计算所交的税款得答案.
解答 解:法一、按原税法计算时,∵500×5%=25<123,
∴所以收入大于500+800=1300(元);
又(2000-500)×=150>123,
∴所以收入小于1500+800+500=2800(元);
该人的税费:123=25+98,980×10%=98,其收入为:800+500+980=2280.
在新的税收标准下,分解其收入为2280=1600+680=1600+500+180,
该人所交税费为500×5%+180×10%=25+18=43元.
故答案为:43.
法二、由f(x)表示此人收入x元时交纳的个人所得税,
则f(x)=$\left\{\begin{array}{l}{0,x∈(0,800]}\\{(x-800)•5%,x∈(800,1300]}\\{25+(x-1300)•10%,x∈(1300,2800]}\\{225+(x-2800)•15%,x∈(2800,5800]}\end{array}\right.$.
某人2005年3月交纳个人所得税123元,则25+(x-1300)•10%=123,解得x=2280.
按新税法此人要交纳个人所得税500×5%+(2280-1600-500)×10%=43元.
故答案为:43.
点评 本题考查函数模型的选择及应用,由表格正确得出此人所交的个人所得税的算法是解题的关键,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
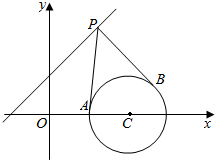 已知直线x-y+2=0和圆C:x2+y2-8x+12=0,过直线上的一点P(x0,y0)作两条直线PA,PB与圆C相切于A,B两点.①当P点坐标为(2,4)时,求以PC为直径的圆的方程,并求直线AB的方程;
已知直线x-y+2=0和圆C:x2+y2-8x+12=0,过直线上的一点P(x0,y0)作两条直线PA,PB与圆C相切于A,B两点.①当P点坐标为(2,4)时,求以PC为直径的圆的方程,并求直线AB的方程;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com