
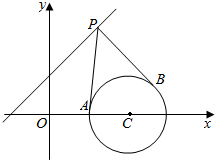
 已知直线x-y+2=0和圆C:x2+y2-8x+12=0,过直线上的一点P(x0,y0)作两条直线PA,PB与圆C相切于A,B两点.①当P点坐标为(2,4)时,求以PC为直径的圆的方程,并求直线AB的方程;
已知直线x-y+2=0和圆C:x2+y2-8x+12=0,过直线上的一点P(x0,y0)作两条直线PA,PB与圆C相切于A,B两点.①当P点坐标为(2,4)时,求以PC为直径的圆的方程,并求直线AB的方程;分析 ①确定P,A,B,C四点共圆E,直线AB的方程是两圆公共弦所在直线方程;
②利用直线与圆相切的充要条件、点到直线的距离公式即可得出.
解答 解:①圆C:x2+y2-8x+12=0,可化为(x-4)2+y2=4,PC中点为(3,2),|PC|=2$\sqrt{5}$,
∴以PC为直径的圆的方程为圆E:(x-3)2+(y-2)2=5,
∵PA⊥AC,PB⊥BC,
∴P,A,B,C四点共圆E,
∴直线AB的方程是两圆公共弦所在直线方程,两方程相减可得直线AB的方程为x-2y-2=0;
②设过P的直线l方程为y-y0=k(x-x0),由于⊙C与直线l相切,得到d=$\frac{|4k+{y}_{0}-k{x}_{0}|}{\sqrt{{k}^{2}+1}}$=2,
整理得到:k2[(4-x0)2-4]+2y0(4-x0)k+y02=4k2+4,
∴k1•k2=$\frac{{{y}_{0}}^{2}-4}{(4-{x}_{0})^{2}-4}$=-7
y0=x0+2,代入,可得2x02-13x0+21=0,∴x0=3或$\frac{7}{2}$,
∴点P坐标(3,5)或($\frac{7}{2}$,$\frac{11}{2}$).
点评 熟练掌握两圆的根轴的性质、直线与圆相切的充要条件、点到直线的距离公式是解题的关键.


科目:高中数学 来源:2017届湖北襄阳四中高三七月周考三数学(文)试卷(解析版) 题型:解答题
选修4-5:不等式选讲
已知函数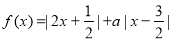 .
.
(1)当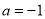 时,解不等式
时,解不等式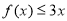 ;
;
(2)当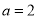 时,若关于
时,若关于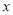 的不等式
的不等式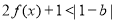 的解集为空集,求实数
的解集为空集,求实数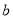 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届湖北襄阳四中高三七月周考三数学(文)试卷(解析版) 题型:解答题
选修4-4:坐标系与参数方程
已知曲线C的极坐标方程是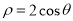 ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是
,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是 (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程和直线L的普通方程;
(2)设点P(m,0),若直线L与曲线C交于两点A,B,且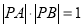 ,求实数m的值.
,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 级数 | 全月应纳税所得额 | 税率(%) |
| 1 | 不超过500元 | 5 |
| 2 | 500~2000元 | 10 |
| 3 | 2000~5000元 | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com