
分析 (1)根据定义构造方程,再判断方程是否有解,问题得以解决.
(2)根据定义构造方程4x+4-x-2m(2x+2-x)+2(m2-3)=0…(*)在R上有解,再利用换元法,设t=2x+2-x,方程变形为t2-2mt+2m2-8=0 在区间[2,+∞)内有解,再根据判别式求出m的范围即可
解答 解:(1)证明:由f(x)=ax3+bx2+cx-b得f(-x)=-ax3+bx2-cx-b,
代入f(-x)=-f(x) 得ax3+bx2+cx-b-ax3+bx2-cx-b=0得到关于x的方程2bx2-2b=0,b≠0时,x=±1
当b=0,x∈R等式恒成立,
所以函数f(x)=ax3+bx2+cx-b必有局部对称点;
(2)∵f(x)=4x-m2x+1+m2-3
∴f(-x)=4-x-m•2-x+1+m2-3,
由f(-x)=-f(x),∴4-x-m•2-x+1+m2-3=-(4x-m•2x+1+m2-3),
于是 4x+4-x-2m(2x+2-x)+2(m2-3)=0…(*)在R上有解,
令t=2x+2-x(t≥2),则4x+4-x=t2-2,
∴方程(*)变为t2-2mt+2m2-8=0 在区间[2,+∞)内有解,需满足条件:
$\left\{\begin{array}{l}△=4{m}^{2}-8({m}^{2}-4)≥0\\ \frac{2m+\sqrt{4(8-{m}^{2})}}{2}≥2\end{array}\right.$,解得$\left\{\begin{array}{l}-2\sqrt{2}≤m≤2\sqrt{2}\\ 1-\sqrt{3}≤m≤2\sqrt{2}\end{array}\right.$,
化简得$1-\sqrt{3}$≤m≤2$\sqrt{2}$.
点评 本题依据新定义,考查了方程的解得问题以及参数的取值范围,以及换元的思想,转化思想,属于难题.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:解答题
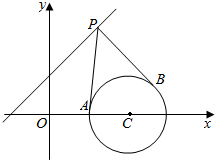 已知直线x-y+2=0和圆C:x2+y2-8x+12=0,过直线上的一点P(x0,y0)作两条直线PA,PB与圆C相切于A,B两点.①当P点坐标为(2,4)时,求以PC为直径的圆的方程,并求直线AB的方程;
已知直线x-y+2=0和圆C:x2+y2-8x+12=0,过直线上的一点P(x0,y0)作两条直线PA,PB与圆C相切于A,B两点.①当P点坐标为(2,4)时,求以PC为直径的圆的方程,并求直线AB的方程;查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 12 | C. | 24 | D. | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com