
| A. | 6 | B. | 12 | C. | 24 | D. | 36 |
分析 运用三点共线的条件可得,O,B,C共线,点O是△ABC的外接圆圆心,即有OA=OB=OC,则AB⊥AC,即有$\overrightarrow{AB}$•$\overrightarrow{AC}$=0,再由向量共线定理可得向量AD,再由向量的数量积的性质计算即可得到所求值.
解答 解:由$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,且x+y=1,
可得O,B,C共线,
点O是△ABC的外接圆圆心,即有OA=OB=OC,
则AB⊥AC,即有$\overrightarrow{AB}$•$\overrightarrow{AC}$=0,
又$\overrightarrow{CD}$=2$\overrightarrow{DB}$,即$\overrightarrow{AD}$-$\overrightarrow{AC}$=2($\overrightarrow{AB}$-$\overrightarrow{AD}$),
可得$\overrightarrow{AD}$=$\frac{\overrightarrow{AC}+2\overrightarrow{AB}}{3}$,
则$\overrightarrow{AB}$•$\overrightarrow{AD}$=$\frac{1}{3}$($\overrightarrow{AB}$•$\overrightarrow{AC}$+2$\overrightarrow{AB}$2)
=$\frac{1}{3}$×(0+2×36)=24.
故选:C.
点评 本题考查向量的数量积的求法,考查三点共线共线的条件,考查三角形外接圆的性质,考查运算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2017届湖北襄阳四中高三七月周考三数学(文)试卷(解析版) 题型:解答题
选修4-4:坐标系与参数方程
已知曲线C的极坐标方程是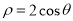 ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是
,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是 (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程和直线L的普通方程;
(2)设点P(m,0),若直线L与曲线C交于两点A,B,且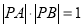 ,求实数m的值.
,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {0} | C. | {(0,1)}和{(1,2)} | D. | {1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{5π}{6}$,$\frac{11π}{6}$] | B. | [$\frac{2π}{3}$,$\frac{5π}{3}$] | C. | [$\frac{π}{2}$,$\frac{3π}{2}$] | D. | [-$\frac{π}{2}$,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
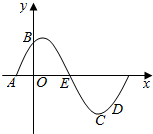 已知A、B、C、D是函数y=sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)一个周期内的图象上的四个点,如图所示,A(-$\frac{π}{6}$,0),B为y轴的点,C为图象上的最低点,E为该函数图象的一个对称中心,B与D关于点E对称,$\overrightarrow{CD}$在x轴方向上的投影为$\frac{π}{12}$.
已知A、B、C、D是函数y=sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)一个周期内的图象上的四个点,如图所示,A(-$\frac{π}{6}$,0),B为y轴的点,C为图象上的最低点,E为该函数图象的一个对称中心,B与D关于点E对称,$\overrightarrow{CD}$在x轴方向上的投影为$\frac{π}{12}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com