
分析 (1)根据函数奇偶性的性质进行求解即可.
(2)根据函数奇偶性和单调性的性质将不等式进行转化求解即可.
解答 解:(1)当x<0时,-x>0,f(x)=-f(-x)=-log2(1-x),…(5分)
当x=0时,由于f(x)为奇函数,f(x)=0.
综上,$f(x)=\left\{{\begin{array}{l}{{{log}_2}(1+x),x>0}\\{0,x=0}\\{-{{log}_2}(1-x),x<0}\end{array}}\right.$.…(7分)
(少了x=0的情况得5分)
(2)f(t2-2t)+f(2t2-5)<0⇒f(t2-2t)<-f(2t2-5),
由于f(x)为奇函数,则f(t2-2t)<f(5-t2),…(9分)
由于f(x)在R上单调递增,则t2-2t<5-2t2⇒3t2-2t-5<0…(11分)
⇒$t∈({-1,\frac{5}{3}})$.…(14分)
点评 本题主要考查函数解析式的求解以及不等式的求解,根据函数奇偶性和单调性的性质是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
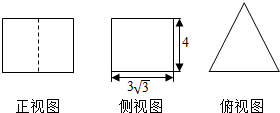 若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图所示,则这个棱柱的表面积为$72+18\sqrt{3}$.则这个棱柱体积为36$\sqrt{3}$.
若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图所示,则这个棱柱的表面积为$72+18\sqrt{3}$.则这个棱柱体积为36$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
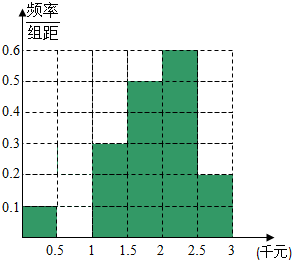 2014年7月16日,中国互联网络信息中心发布《第三十四次中国互联网发展状况报告》,报告显示:我国网络购物用户已达3.32亿.为了了解网购者一次性购物金额情况,某统计部门随机抽查了6月1日这一天100名网购者的网购情况,得到如下数据统计表.已知网购金额在2000元以上(不含2000元)的频率为0.4.
2014年7月16日,中国互联网络信息中心发布《第三十四次中国互联网发展状况报告》,报告显示:我国网络购物用户已达3.32亿.为了了解网购者一次性购物金额情况,某统计部门随机抽查了6月1日这一天100名网购者的网购情况,得到如下数据统计表.已知网购金额在2000元以上(不含2000元)的频率为0.4.| 网购金额 (单位:元) | 频数 | 频率 |
| (0,500] | 5 | 0.05 |
| (500,1000] | x | p |
| (1000,1500] | 15 | 0.15 |
| (1500,2000] | 25 | 0.25 |
| (2000,2500] | 30 | 0.30 |
| (2500,3000] | y | q |
| 合计 | 100 | 1.00 |
| 网龄3年以上 | 网龄不足3年 | 合计 | |
| 购物金额在2000元以上 | 35 | ||
| 购物金额在2000元以下 | 20 | ||
| 合计 | 100 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某几何体的三视图如图所示,则这个几何体的体积为( )
某几何体的三视图如图所示,则这个几何体的体积为( )| A. | $\frac{\sqrt{3}}{6}$π | B. | $\frac{\sqrt{3}}{2}π$ | C. | $\frac{2\sqrt{3}}{3}π$ | D. | $\frac{4\sqrt{3}}{3}π$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com