
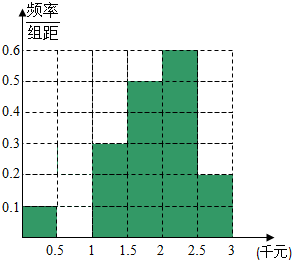
 2014年7月16日,中国互联网络信息中心发布《第三十四次中国互联网发展状况报告》,报告显示:我国网络购物用户已达3.32亿.为了了解网购者一次性购物金额情况,某统计部门随机抽查了6月1日这一天100名网购者的网购情况,得到如下数据统计表.已知网购金额在2000元以上(不含2000元)的频率为0.4.
2014年7月16日,中国互联网络信息中心发布《第三十四次中国互联网发展状况报告》,报告显示:我国网络购物用户已达3.32亿.为了了解网购者一次性购物金额情况,某统计部门随机抽查了6月1日这一天100名网购者的网购情况,得到如下数据统计表.已知网购金额在2000元以上(不含2000元)的频率为0.4.| 网购金额 (单位:元) | 频数 | 频率 |
| (0,500] | 5 | 0.05 |
| (500,1000] | x | p |
| (1000,1500] | 15 | 0.15 |
| (1500,2000] | 25 | 0.25 |
| (2000,2500] | 30 | 0.30 |
| (2500,3000] | y | q |
| 合计 | 100 | 1.00 |
| 网龄3年以上 | 网龄不足3年 | 合计 | |
| 购物金额在2000元以上 | 35 | ||
| 购物金额在2000元以下 | 20 | ||
| 合计 | 100 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)求出网购金额在2000元以上的人数,可得x,y的值,由此能求出x,y,p,q的值,并补全频率分布直方图.
(2)由数据可得列联表,利用公式,可得结论.
解答  解:(1)因为网购金额在2000元以上的频率为0.4,
解:(1)因为网购金额在2000元以上的频率为0.4,
所以网购金额在2000元以上的人数为100×0.4=40
所以30+y=40,所以y=10,…(1分)x=15,…(2分)
所以p=0.15,q=0.1…(4分)
所以频率分布直方图如图…(5分)
(2)由题设列联表如下
| 网龄3年以上 | 网龄不足3年 | 合计 | |
| 购物金额在2000元以上 | 35 | 5 | 40 |
| 购物金额在2000元以下 | 40 | 20 | 60 |
| 合计 | 75 | 25 | 100 |
点评 本题考查频率分布直方图,考查独立性检验的运用,考查学生的计算能力,属于中档题.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2] | B. | [2,+∞) | C. | (-∞,2] | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
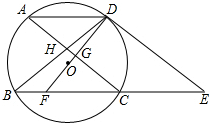 如图,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及延长线分别交AC,BC于点G,F.
如图,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及延长线分别交AC,BC于点G,F.查看答案和解析>>
科目:高中数学 来源:2017届湖北襄阳四中高三七月周考三数学(文)试卷(解析版) 题型:解答题
已知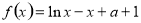 .
.
(1)若存在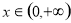 使得
使得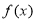 ≥0成立,求
≥0成立,求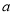 的范围;
的范围;
(2)求证:当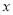 >1时,在(1)的条件下,
>1时,在(1)的条件下,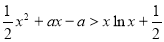 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com