
分析 (Ⅰ)将a=0代入不等式,得到关于x的不等式组,解出即可;
(Ⅱ)通过讨论a的范围,求出f(x)的分段函数,从而求出函数的单调区间;
(Ⅲ)先求出函数的值域,结合换元法以及a的范围,求出方程的解即可.
解答 解:(Ⅰ)当a=0时,不等式f(x)<2,即:${e^x}+|{\frac{1}{e^x}-1}|<2$,
即$|{\frac{1}{e^x}-1}|<2-{e^x}$,因此$\left\{\begin{array}{l}\frac{1}{e^x}-1>{e^x}-2\\ \frac{1}{e^x}-1<2-{e^x}\end{array}\right.$…(2分)
得$\frac{{3-\sqrt{5}}}{2}<{e^x}<\frac{{1+\sqrt{5}}}{2}$,所以$ln\frac{{3-\sqrt{5}}}{2}<x<ln\frac{{1+\sqrt{5}}}{2}$,
所以原不等式的解集为$(ln\frac{{3-\sqrt{5}}}{2},ln\frac{{1+\sqrt{5}}}{2})$.…(4分)
(Ⅱ)①当a≤0时,$f(x)={e^x}-a+|{\frac{1}{e^x}-1}|=\left\{\begin{array}{l}{e^x}-\frac{1}{e^x}-a+1,x≥0\\{e^x}+\frac{1}{e^x}-a-1,x<0.\end{array}\right.$
因为x>0时,$f'(x)={e^x}+\frac{1}{e^x}>0$,x<0时,$f(x)={e^x}-\frac{1}{e^x}<0$,
故f(x)在区间(-∞,0)上单调递减,在区间(0,+∞)上单调递增;…(5分)
②当0<a<1时,$f(x)=\left\{\begin{array}{l}{e^x}-\frac{1}{e^x}-a+1,x≥0\\{e^x}+\frac{1}{e^x}-a-1,lna<x<0\\-{e^x}+\frac{1}{e^x}+a-1,x≤lna.\end{array}\right.$,
仿①得f(x)在(-∞,lna)和(lna,0)上单调递减,在(0,+∞)上单调递增,
即f(x)在区间(-∞,0)上单调递减,在区间(0,+∞)上单调递增;(6分)
③当a=1时,$f(x)=\left\{\begin{array}{l}{e^x}-\frac{1}{e^x},x≥0\\ \frac{1}{e^x}-{e^x},x<0\end{array}\right.$
易得f(x)在区间(-∞,0)上单调递减,在区间(0,+∞)上单调递增; …(7分)
④当a>1时,$f(x)=\left\{\begin{array}{l}{e^x}-\frac{1}{e^x}-a+1,x≥lna\\-{e^x}-\frac{1}{e^x}+a+1,0<x<lna\\-{e^x}+\frac{1}{e^x}+a-1,x≤0.\end{array}\right.$
同理得f(x)在区间(-∞,lna)上单调递减,在区间(lna,+∞)上单调递增.…(8分)
综上所述,
当a≤1时,f(x)在区间(-∞,0)上单调递减,在区间(0,+∞)上单调递增;
当a>1时,f(x)在区间(-∞,lna)上单调递减,在区间(lna,+∞)上单调递增.…(10分)
(Ⅲ)由(Ⅱ)知:当$a≥\frac{4}{3}$时,因为$f(lna)={e^{lna}}-\frac{1}{{{e^{lna}}}}-a+1=1-\frac{1}{a}$,
又x→+∞时,${e^x}-\frac{1}{e^x}-a+1→+∞$,
所以f(x)的值域为$[1-\frac{1}{a},+∞)$,且$1>1-\frac{1}{a}≥\frac{1}{4}$(等号仅当$a=\frac{4}{3}$时取).…(12分)
令$f(x)=u,f(u)=\frac{1}{4}$,
当$a>\frac{4}{3}$时,$f(u)>\frac{1}{4}$,所以$f(u)=\frac{1}{4}$不成立,原方程无解;…(13分)
当$a=\frac{4}{3}$时,由$f(u)=\frac{1}{4}$得$u=ln\frac{4}{3}$,因为$ln{(\frac{4}{3})^4}=ln\frac{256}{81}>ln3>1$,所以$ln\frac{4}{3}>\frac{1}{4}$,
所以$f(x)=ln\frac{4}{3}$有两个不相等的实数根,故原方程有两个不同的实数解.…(15分)
综上所述,当$a>\frac{4}{3}$时,原方程无解;当$a=\frac{4}{3}$时,原方程有两个不同的实数解.(16分).
点评 本题考查了不等式的性质,考查函数的单调性以及方程的解的问题,是一道综合题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\sqrt{5}$ | C. | ±$\sqrt{5}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
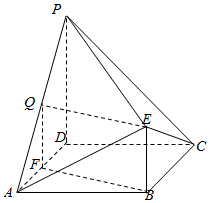 如图所示几何体中,底面ABCD是正方形,PD⊥平面ABCD,BE∥PD,AB=PD=2BE=2,F为AD的中点.
如图所示几何体中,底面ABCD是正方形,PD⊥平面ABCD,BE∥PD,AB=PD=2BE=2,F为AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com