
【题目】如图,已知焦点在x轴上的椭圆![]() 有一个内含圆x2+y2=
有一个内含圆x2+y2=![]() ,该圆的垂直于x轴的切线交椭圆于点M,N,且
,该圆的垂直于x轴的切线交椭圆于点M,N,且![]() (O为原点).
(O为原点).

(1)求b的值;
(2)设内含圆的任意切线l交椭圆于点A、B.求证:![]() ,并求|AB|的取值范围.
,并求|AB|的取值范围.
【答案】(1)2;(2)证明见解析,![]() .
.
【解析】
(1)设![]() 的坐标,利用
的坐标,利用![]() ,求得
,求得![]() ,得到点
,得到点![]() 代入椭圆的方程,即可求解;
代入椭圆的方程,即可求解;
(2)分类讨论,当![]() 轴时,由(1)知
轴时,由(1)知![]() ;当
;当![]() 不与
不与![]() 轴垂直时,设
轴垂直时,设![]() 的方程为
的方程为![]() ,代入椭圆的方程,利用韦达定理证得
,代入椭圆的方程,利用韦达定理证得![]() ,再利用弦长公式,结合换元法和二次函数的性质,即可求解.
,再利用弦长公式,结合换元法和二次函数的性质,即可求解.
(1)由圆![]() 的垂直于x轴的切线交椭圆于点M,N,,
的垂直于x轴的切线交椭圆于点M,N,,
可得直线![]() 的方程为
的方程为![]() ,
,
设![]() ,
,
由![]() ,即
,即![]() ,解得
,解得![]() ,
,
可得点![]() 在椭圆上,代入椭圆方程
在椭圆上,代入椭圆方程![]() ,
,
可得![]() .
.
(2)当![]() 轴时,由(1)知
轴时,由(1)知![]() ,
,
当![]() 不与
不与![]() 轴垂直时,设
轴垂直时,设![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
则原点到直线的距离,可得![]() ,整理得
,整理得![]() ,
,
把直线![]() 代入椭圆的方程
代入椭圆的方程![]() ,
,
整理得![]() ,
,
则![]() ,
,
设![]() ,则
,则![]() ,
,
所以![]() ,即
,即![]() ,
,
即椭圆内含圆![]() 的任意切线
的任意切线![]() 交椭圆
交椭圆![]() 时,总有
时,总有![]() ,
,
当![]() 轴时,可得
轴时,可得![]() ;
;
当![]() 不与
不与![]() 轴垂直时,可得
轴垂直时,可得 ,
,
设![]() ,则
,则![]() ,
,
则![]() ,
,
所以当![]() ,即
,即![]() 时,
时,![]() 的取最大值
的取最大值![]() ,
,
当![]() ,即
,即![]() 时,
时,![]() 的取最小值
的取最小值![]() ,
,
综上可得,![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】为响应德智体美劳的教育方针,唐徕回中高一年级举行了由全体学生参加的一分钟跳绳比赛,计分规则如下:
每分钟跳绳个数 |
|
|
|
| 185以上 |
得分 | 16 | 17 | 18 | 19 | 20 |
年级组为了了解学生的体质,随机抽取了100名学生,统计了他的跳绳个数,并绘制了如下样本频率直方图:
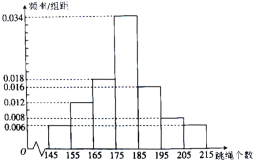
(1)现从这100名学生中,任意抽取2人,求两人得分之和小于35分的概率(结果用最简分数表示);
(2)若该校高二年级2000名学生,所有学生的一分钟跳绳个数![]() 近似服从正态分布
近似服从正态分布![]() ,其中
,其中![]() ,
,![]() 为样本平均数的估计值(同一组中数据以这组数据所在区间的中点值为代表).利用所得到的正态分布模型解决以下问题:
为样本平均数的估计值(同一组中数据以这组数据所在区间的中点值为代表).利用所得到的正态分布模型解决以下问题:
①估计每分钟跳绳164个以上的人数(四舍五入到整数)
②若在全年级所有学生中随机抽取3人,记每分钟跳绳在179个以上的人数为![]() ,求
,求![]() 的分布列和数学期望与方差.
的分布列和数学期望与方差.
(若随机变量![]() 服从正态分布
服从正态分布![]() 则
则![]() ,
,![]() ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某媒体为调查喜爱娱乐节目A是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
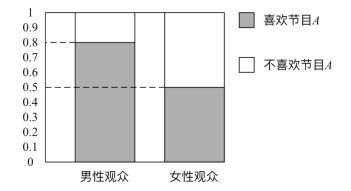
根据该等高条形图,完成下列2×2列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过0.05的前提下认为喜欢娱乐节目A与观众性别有关?
喜欢节目A | 不喜欢节目A | 总计 | |
男性观众 | |||
女性观众 | |||
总计 | 60 |
附: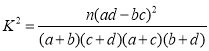
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某地区2000年至2016年环境基础设施投资额![]() (单位:亿元)的折线图.则下列结论中表述不正确的是( )
(单位:亿元)的折线图.则下列结论中表述不正确的是( )
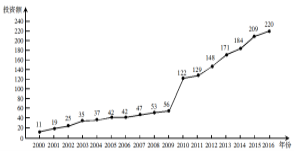
A. 从2000年至2016年,该地区环境基础设施投资额逐年增加;
B. 2011年该地区环境基础设施的投资额比2000年至2004年的投资总额还多;
C. 2012年该地区基础设施的投资额比2004年的投资额翻了两番 ;
D. 为了预测该地区2019年的环境基础设施投资额,根据2010年至2016年的数据(时间变量t的值依次为![]() )建立了投资额y与时间变量t的线性回归模型
)建立了投资额y与时间变量t的线性回归模型![]() ,根据该模型预测该地区2019的环境基础设施投资额为256.5亿元.
,根据该模型预测该地区2019的环境基础设施投资额为256.5亿元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右顶点为A,下顶点为B,过A、O、B(O为坐标原点)三点的圆的圆心坐标为
的右顶点为A,下顶点为B,过A、O、B(O为坐标原点)三点的圆的圆心坐标为![]() .
.
(1)求椭圆的方程;
(2)已知点M在x轴正半轴上,过点B作BM的垂线与椭圆交于另一点N,若∠BMN=60°,求点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com