
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 本题考查的知识点是简单的线性规划,我们可以先画出足约束条件$\left\{\begin{array}{l}x≤a\\ y≤2\\ x+y≥2\end{array}\right.$的平面区域,再根据目标函数z=x+2y的最大值是6,求出点的横坐标即可.
解答 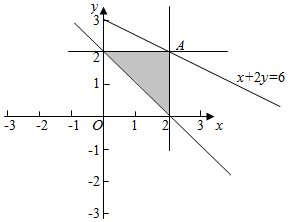 解:满足约束条件$\left\{\begin{array}{l}x≤a\\ y≤2\\ x+y≥2\end{array}\right.$的平面区域如下图:
解:满足约束条件$\left\{\begin{array}{l}x≤a\\ y≤2\\ x+y≥2\end{array}\right.$的平面区域如下图:
∵目标函数z=x+2y的最大值是6,
可得$\left\{\begin{array}{l}{x+2y=6}\\{y=2}\end{array}\right.$,可得A(2,2).
∴当x=2,y=2时,Z取最大值6,
A(2,2)在直线x=a上,可得a=2,
故选:A.
点评 用图解法解决线性规划问题时,分析题目的已知条件,找出约束条件和目标函数是关键,可先将题目中的量分类、列出表格,理清头绪,然后列出不等式组(方程组)寻求约束条件,并就题目所述找出目标函数.然后将可行域各角点的值一一代入,最后比较,即可得到目标函数的最优解.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
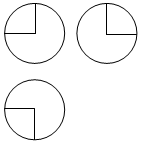 如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是$\frac{28π}{3}$,则它的表面积是( )
如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是$\frac{28π}{3}$,则它的表面积是( )| A. | 17π | B. | 18π | C. | 20π | D. | 28π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
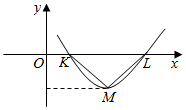 设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,△KLM为等腰直角三角形,∠KML=90°,KL=1,则f($\frac{1}{12}$)的值为( )
设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,△KLM为等腰直角三角形,∠KML=90°,KL=1,则f($\frac{1}{12}$)的值为( )| A. | $\frac{\sqrt{6}-\sqrt{2}}{8}$ | B. | $\frac{\sqrt{2}+\sqrt{6}}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{\sqrt{3}}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com