
分析 ${a_{n+1}}-{a_n}<{2^n}+\frac{1}{2}$,可得${a_{n+2}}-{a_{n+1}}<{2^{n+1}}+\frac{1}{2}$,两式左右两边分别相加得an+2-an<3×2n+1,又${a_{n+2}}-{a_n}>3×{2^n}-1$,且n∈N*,可得${a_{n+2}}-{a_n}=3×{2^n}$,从而a2019=(a2019-a2017)+(a2017-a2015)…+(a3-a1)+a1=22019=(3-1)2019,利用二项式定理展开即可得出.
解答 解:${a_{n+1}}-{a_n}<{2^n}+\frac{1}{2}$,所以${a_{n+2}}-{a_{n+1}}<{2^{n+1}}+\frac{1}{2}$,
两式左右两边分别相加得an+2-an<3×2n+1,
又${a_{n+2}}-{a_n}>3×{2^n}-1$,且n∈N*,
所以${a_{n+2}}-{a_n}=3×{2^n}$,
从而a2019=(a2019-a2017)+(a2017-a2015)…+(a3-a1)+a1
=3(22017+22015+…+2)+2=$3×2×\frac{{4}^{1009}-1}{4-1}$+2=22019=(3-1)2019=${3}^{2019}-{∁}_{2019}^{1}{3}^{2018}$+…+${∁}_{2019}^{2018}$•3-1
=3(32018-2019×32017+…)-3+2,
所以a2019被3除所得余数为2.
故答案为:2.
点评 本题考查了等比数列的通项公式与求和公式、数列递推关系、二项式定理的应用、整除的性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| x | 10 | 15 | 20 | 25 | 30 |
| y | 1 003 | 1 005 | 1 010 | 1 011 | 1 014 |
| A. | $\widehat{y}$=0.56x+997.4 | B. | $\widehat{y}$=0.63x-231.2 | C. | $\widehat{y}$=0.56x+501.4 | D. | $\widehat{y}$=60.4x+400.7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
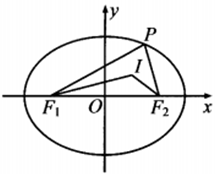 设P为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上的动点,F1、F2为椭圆C的焦点,I为△PF1F2的内心,则直线IF1和直线IF2的斜率之积( )
设P为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上的动点,F1、F2为椭圆C的焦点,I为△PF1F2的内心,则直线IF1和直线IF2的斜率之积( )| A. | 是定值 | B. | 非定值,但存在最大值 | ||
| C. | 非定值,但存在最小值 | D. | 非定值,且不存在最值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com