已知函数f(x)=ax+k(a>0且a≠1)的图象过点(-1,1),其反函数f-1(x)的图象过点(8,2).(1)求a,k的值
(2)若将y=f-1(x)的图象向左平移2个单位,再向上平移1个单位,就得到函数y=g(x)的图象,写出y=g(x)的解析式
(3)若函数F(x)=g(x2)-f-1(x),求F(x)的最小值及取得最小值时x的值.
【答案】
分析:(1)由函数f(x)=a
x+k(a>0且a≠1)的图象过点(-1,1),f(-1)=a
-1+k=1,解得k=1.函数f(x)=a
x+k反函数f
-1(x)的图象过点(8,2),知a
2+k=8,解得a=2.
(2)由(1)得f(x)=2
x+1,所以f
-1(x)=log
2x-1.由此解得g(x)=log
2(x+2).(x>-2)
(3)由f(x)=g(x
2)-f
-1(x),知f(x)=
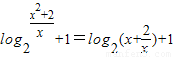
,由此能求出当且仅当
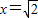
时取
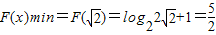
.
解答:解:(1)∵函数f(x)=a
x+k(a>0且a≠1)的图象过点(-1,1),
∴f(-1)=a
-1+k=1,
解得k=1.
∵函数f(x)=a
x+k反函数f
-1(x)的图象过点(8,2),
∴函数f(x)=a
x+k的图象过点(2,8),
∴a
2+k=8,即a
3=8,
∴a=2.
(2)由(1)得f(x)=2
x+1,
∴f
-1(x)=log
2x-1.
将y=f
-1(x)的图象向左移2,向上移1得f
-1(x+2)-1=log
2(x+2),
∴g(x)=log
2(x+2).(x>-2)
(3)f(x)=g(x
2)-f
-1(x)
=log
2(x
2+2)-log
2x+1(x>0)
=
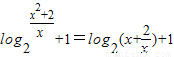
,
∴x>0,
∴
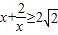
,
当且仅当
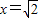
时取
∴
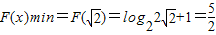
.
点评:本题考查反函数的性质和应用,对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错.解题时要认真审题,仔细解答,注意合理地进行等价转化.

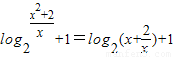 ,由此能求出当且仅当
,由此能求出当且仅当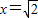 时取
时取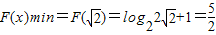 .
.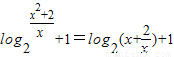 ,
,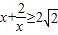 ,
,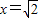 时取
时取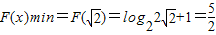 .
.

 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案