
分析 利用二倍角正弦把等式右边变形,然后结合不等式成立的条件可得答案.
解答 解:由方程cos2x+cos22x+cos24x+cos28x=$\sqrt{\frac{sin16x}{sinx}}$,
得:cos2x+cos22x+cos24x+cos28x=4$\sqrt{cosx•cos2x•cos4x•cos8x}$=4$\sqrt{|cosx•cos2x•cos4x•cos8x|}$,
∵cos2x+cos22x+cos24x+cos28x$≥4\root{4}{co{s}^{2}x•co{s}^{2}2x•co{s}^{2}4x•co{s}^{2}8x}$=$4\sqrt{|cosx•cos2x•cos4x•cos8x|}$.
当且仅当cos2x=cos22x=cos24x=cos28x,即|cosx|=|cos2x|=cos4x|=cos8x|时上式“=”成立.
∴x=2kπ,k∈Z.
∴方程cos2x+cos22x+cos24x+cos28x=$\sqrt{\frac{sin16x}{sinx}}$的解集是{x|x=2kπ,k∈Z}.
故答案为:{x|x=2kπ,k∈Z}.
点评 本题考查三角函数中的恒等变换应用,考查了基本不等式成立的条件,考查了三角函数的求值,是中档题.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届广东华南师大附中高三综合测试一数学(理)试卷(解析版) 题型:选择题
已知函数 是定义在
是定义在 上的以4为周期的函数,当
上的以4为周期的函数,当 时,
时, ,其中
,其中 .若函数
.若函数 的零点个数是5,则
的零点个数是5,则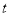 的取值范围为( )
的取值范围为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 1+2 | C. | 1+2+22 | D. | 1+2+22+23 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com