
分析 构造函数F(x)=$\frac{{x}^{2}f(x)}{{e}^{x}}$ (x<0),求函数的导数,利用导数判断其单调性,结合函数为奇函数,即可得出结论.
解答 解:构造函数F(x)=$\frac{{x}^{2}f(x)}{{e}^{x}}$ (x<0),
则F′(x)=$\frac{2xf(x){e}^{x}+{x}^{2}f′(x){e}^{x}-{x}^{2}f(x){e}^{x}}{{(e}^{x})^{2}}$=$\frac{x[2f(x)+xf′(x)-xf(x)]}{{e}^{x}}$,
∵当x<0时,f(x)满足2f(x)+xf′(x)<xf(x),
∴F′(x)>0,
即函数F(x)在x<0时是增函数,
又F(0)=0,
∴当x<0,F(x)<F(0)=0成立,
∵对任意x<0,$\frac{{x}^{2}}{{e}^{x}}$>0,∴f(x)<0,
∵f(x)是奇函数,
∴x>0时,f(x)>0,
即f(x)=0只有一个根就是0.
故答案为:0
点评 本题考查了函数零点个数求解;根据条件构造函数F(x)=$\frac{{x}^{2}f(x)}{{e}^{x}}$是解决本题的关键.综合考查函数单调性和导数的关系.


科目:高中数学 来源:2017届广东华南师大附中高三综合测试一数学(文)试卷(解析版) 题型:解答题
在三角形 中,角
中,角 的对边分别为
的对边分别为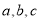 ,且三角形的面积为
,且三角形的面积为 .
.
(1)求角 的大小;
的大小;
(2)已知 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
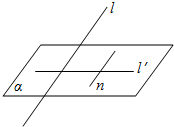 如图,设直线l是平面α的一条射线,l′是l在α内的射影,直线n?α.用<a,b>表示直线a,b的夹角.求证:
如图,设直线l是平面α的一条射线,l′是l在α内的射影,直线n?α.用<a,b>表示直线a,b的夹角.求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | a<0,b<0,c<0 | B. | a>0,b>0,c<0 | C. | a>0,b<0,c>0 | D. | a>0,b>0,c>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,1)∪(1,$\sqrt{2}$) | C. | (1,$\sqrt{2}$) | D. | ($\sqrt{2}$,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com