
设p:函数f(x)=2|x-a|在区间(4,+∞)上单调递增;q:loga2<1.如果“非p”是真命题,“p或q”也是真命题,那么实数a的取值范围是________.
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:
已知集合P={3,log2a},Q={a,b},若P∩Q={0},则P∪Q等于( )
A.{3,0} B.{3,0,1}
C.{3,0,2} D.{3,0,1,2}
查看答案和解析>>
科目:高中数学 来源: 题型:
设数集M={x|m≤x≤m+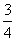 },N={x|n-
},N={x|n-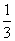 ≤x≤n},且M,N都是集合{x|0≤x≤1}的子集,如果把b-a叫做集合{x|a≤x≤b}的“长度”,那么集合M∩N的“长度”的最小值是( )
≤x≤n},且M,N都是集合{x|0≤x≤1}的子集,如果把b-a叫做集合{x|a≤x≤b}的“长度”,那么集合M∩N的“长度”的最小值是( )
A.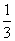 B.
B.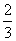
C.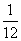 D.
D.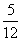
查看答案和解析>>
科目:高中数学 来源: 题型:
命题“∃x∈R,2x+x2≤1”的否定是( )
A.∀x∈R,2x+x2>1,假命题
B.∀x∈R,2x+x2>1,真命题
C.∃x∈R,2x+x2>1,假命题
D.∃x∈R,2x+x2>1,真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
下列命题:
①∀x∈R,不等式x2+2x>4x-3均成立;
②若log2x+logx2≥2,则x>1;
③“若a>b>0且c<0,则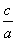 >
>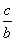 ”的逆否命题是真命题;
”的逆否命题是真命题;
④若命题p:∀x∈R,x2+1≥1,命题q:∃x∈R,x2-x-1≤0,则命题p∧(綈q)是真命题.其中真命题为( )
A.①②③ B.①②④
C.①③④ D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
已知a、b、c是三条不同的直线,命题“a∥b且a⊥c⇒b⊥c”是正确的,如果把a、b、c中的两个或三个换成平面,在所得的命题中,真命题有( )
A.1个 B.2个
C.3个 D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
已知二次函数f(x)有两个零点0和-2,且f(x)最小值是-1,函数g(x)与f(x)的图像关于原点对称.
(1)求f(x)和g(x)的解析式;
(2)若h(x)=f(x)-λg(x)在区间[-1,1]上是增函数,求实数λ的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com