练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    用数学归纳法证明：12＋22＋…＋n2＋…＋22＋12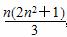＝，第二步证明由“k到k＋1”时，左边应加(　　)

    A．k2                                                            B．(k＋1)2

    C．k2＋(k＋1)2＋k2                                       D．(k＋1)2＋k2


    D


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    某算法的程序框图如图所示，其中输入的变量x在1,2,3，…，24这24个整数中等可能随机产生．

    (1)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i＝1,2,3)；

    (2)甲、乙两同学依据自己对程序框图的理解，各自编写程序重复运行n次后，统计记录了输出y的值为i(i＝1,2,3)的频数，以下是甲、乙所作频数统计表的部分数据．

    甲的频数统计表(部分)

    乙的频数统计表(部分)

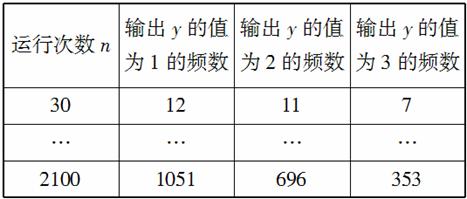
    当n＝2100时，根据表中的数据，分别写出甲、乙所编程序各自输出y的值为i(i＝1,2,3)的频率(用分数表示)，并判断两位同学中哪一位所编程序符合算法要求的可能性较大；

    (3)将按程序框图正确编写的程序运行3次，求输出y的值为2的次数ξ的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    n个连续自然数按规律排成下表：

    根据规律，从2012到2014的箭头方向依次为(　　)

    A．↓→                                                        B．→↑ 

    C．↑→                                                        D．→↓

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知P(x0，y0)是抛物线y2＝2px(p>0)上的一点，过P点的切线方程的斜率可通过如下方式求得：在y2＝2px两边同时对x求导，得2yy′＝2p，则y′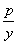＝，所以过P的切线的斜率k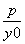＝.类比上述方法求出双曲线x2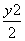－＝1在P(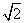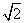，)处的切线方程为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    对于大于或等于2的自然数n的二次方幂有如下分解方式：22＝1＋3,32＝1＋3＋5,42＝1＋3＋5＋7，…，根据上述分解规律，对任意自然数n，当n≥2时，有____________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知n∈N*，设平面上的n个椭圆最多能把平面分成an部分，则a1＝2，a2＝6，a3＝14，a4＝26，…，则an＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    对于不等式≤n＋1(n∈N*)，某人的证明过程如下：

    1°当n＝1时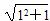，≤1＋1，不等式成立.

    2°假设n＝k(k∈N*)时不等式成立，即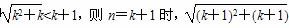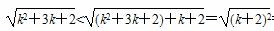＝＝(k＋1)＋1.

    ∴当n＝k＋1时，不等式成立.

    上述证法(　　)

    A．过程全都正确

    B．n＝1验得不正确

    C．归纳假设不正确

    D．从n＝k到n＝k＋1的推理不正确

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，PA切圆O于点A，割线PBC经过圆心O，OB＝PB＝1，OA绕点O逆时针旋转60°到OD，则PD的长为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在极坐标系中，设P是直线l：ρ(cosθ＋sinθ)＝4上任一点，Q是圆C：ρ2＝4ρcosθ－3上任一点，则|PQ|的最小值是________．

    查看答案和解析>>

    同步练习册答案