
已知n∈N*,设平面上的n个椭圆最多能把平面分成an部分,则a1=2,a2=6,a3=14,a4=26,…,则an=________.
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:高中数学 来源: 题型:
已知抛物线y=ax2+bx+c(a≠0)的对称轴在y轴的左侧,其中a、b、c∈{-3,-2,-1,0,1,2,3},在这些抛物线中,记随机变量ξ=“|a-b|的取值”,则ξ的数学期望E(ξ)为( )
A.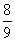 B.
B.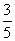
C.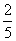 D.
D.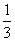
查看答案和解析>>
科目:高中数学 来源: 题型:
设f(x)定义如表,数列{xn}满足x1=5,xn+1=f(xn),则x2014的值为________.
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| f(x) | 4 | 5 | 1 | 2 | 6 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
观察①sin210°+cos240°+sin10°cos40°=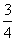 ;
;
②sin26°+cos236°+sin6°cos36°=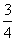 .
.
由上面两题的结构规律,你能否提出一个猜想?并证明你的猜想.
查看答案和解析>>
科目:高中数学 来源: 题型:
用数学归纳法证明:12+22+…+n2+…+22+12=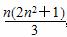 ,第二步证明由“k到k+1”时,左边应加( )
,第二步证明由“k到k+1”时,左边应加( )
A.k2 B.(k+1)2
C.k2+(k+1)2+k2 D.(k+1)2+k2
查看答案和解析>>
科目:高中数学 来源: 题型:
设数列{an}的前n项和为Sn,对一切n∈N*,点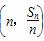 都在函数f(x)=x+
都在函数f(x)=x+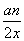 的图象上.
的图象上.
(1)求a1、a2、a3的值,猜想an的表达式,并用数学归纳法证明;
(2)将数列{an}依次按1项、2项、3项、4项循环地分为(a1),(a2,a3),(a4,a5,a6),(a7,a8,a9,a10);(a11),(a12,a13),(a14,a15,a16),(a17,a18,a19,a20);(a21),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为{bn},求b5+b100的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,⊙O是△ABC的外接圆,过⊙O上一点H作⊙O的切线,BC与这条线切线平行,AC、AB的延长线交这条切线于点E、F,连接AH、CH.

(1)求证:AH平分∠EAF;
(2)若CH=4,∠CAB=60°,求圆弧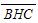 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知直线l是过点P(-1,2),方向向量为n=(-1,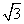 )的直线,圆方程ρ=2cos(θ+
)的直线,圆方程ρ=2cos(θ+ ).
).
(1)求直线l的参数方程;
(2)设直线l与圆相交于M,N两点,求|PM|·|PN|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com