练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在极坐标系中，设P是直线l：ρ(cosθ＋sinθ)＝4上任一点，Q是圆C：ρ2＝4ρcosθ－3上任一点，则|PQ|的最小值是________．


    －1

    [解析]　直线l方程化为x＋y－4＝0，

    ⊙C方程化为x2＋y2－4x＋3＝0，

    即(x－2)2＋y2＝1.

    圆心C(2,0)到直线l的距离d＝＝，

    ∴|PQ|min＝－1.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    用数学归纳法证明：12＋22＋…＋n2＋…＋22＋12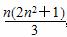＝，第二步证明由“k到k＋1”时，左边应加(　　)

    A．k2                                                            B．(k＋1)2

    C．k2＋(k＋1)2＋k2                                       D．(k＋1)2＋k2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，AB是圆O的直径，延长AB至C，使BC＝2OB，CD是圆O的切线，切点为D，连接AD、BD，则的值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在极坐标系中，过点(2，)且与极轴平行的直线的方程是(　　)

    A．ρcosθ＝                                             B．ρsinθ＝

    C．ρ＝cosθ                                             D．ρ＝sinθ

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在极坐标系中，圆ρ＝4cosθ的圆心C到直线ρsin(θ＋)＝2的距离为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知直线l是过点P(－1,2)，方向向量为n＝(－1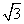，)的直线，圆方程ρ＝2cos(θ＋)．

    (1)求直线l的参数方程；

    (2)设直线l与圆相交于M，N两点，求|PM|·|PN|的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在直角坐标系中，以原点O为极点，x轴的正半轴为极轴，建立极坐标系，设曲线C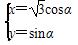：(α为参数)，直线l：ρ(cosθ＋sinθ)＝4.

    (1)写出曲线C的普通方程和直线l的直角坐标方程；

    (2)求曲线C上的点到直线l的最大距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    不等式|2x＋1|＋|x－1|<2的解集为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如果执行如图的框图，输入N＝5，则输出的数等于(　　)

    A.                                                             B.

    C.                                                              D.

    查看答案和解析>>

    同步练习册答案