已知P(x0，y0)是抛物线y2＝2px(p>0)上的一点，过P点的切线方程的斜率可通过如下方式求得：在y2＝2px两边同时对x求导，得2yy′＝2p，则y′＝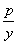
，所以过P的切线的斜率k＝
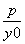.类比上述方法求出双曲线x2－
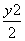＝1在P(
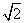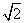，)处的切线方程为________．
科目：高中数学 来源： 题型：
一套重要资料锁在一个保险柜中，现有n把钥匙依次分给n名学生依次开柜，但其中只有一把真的可以打开柜门，平均来说打开柜门需要试开的次数为( )
A．1 B．n
C.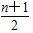 
D.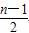 
查看答案和解析>>
科目：高中数学 来源： 题型：
设复数z＝lg(m2－2m－2)＋(m2＋3m＋2)i，当实数m取何值时．
(1)z是纯虚数．
(2)z是实数．
(3)z对应的点位于复平面的第二象限．
查看答案和解析>>
科目：高中数学 来源： 题型：
设f(x)定义如表，数列{xn}满足x1＝5，xn＋1＝f(xn)，则x2014的值为________.
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| f(x) | 4 | 5 | 1 | 2 | 6 | 3 |
查看答案和解析>>
科目：高中数学 来源： 题型：
观察(x2)′＝2x，(x4)′＝4x3，(cosx)′＝－sinx，由归纳推理可得：若定义在R上的函数f(x)满足f(－x)＝f(x)，记g(x)为f(x)的导函数，则g(－x)＝( )
A．f(x) B．－f(x)
C．g(x) D．－g(x)
查看答案和解析>>
科目：高中数学 来源： 题型：
观察①sin210°＋cos240°＋sin10°cos40°＝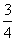
；
②sin26°＋cos236°＋sin6°cos36°＝.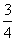
由上面两题的结构规律，你能否提出一个猜想？并证明你的猜想．
查看答案和解析>>
科目：高中数学 来源： 题型：
用数学归纳法证明：12＋22＋…＋n2＋…＋22＋12＝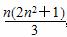
，第二步证明由“k到k＋1”时，左边应加( )
A．k2 B．(k＋1)2
C．k2＋(k＋1)2＋k2 D．(k＋1)2＋k2
查看答案和解析>>
科目：高中数学 来源： 题型：
设数列{an}的前n项和为Sn，对一切n∈N*，点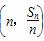
都在函数f(x)＝x＋
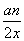的图象上．
(1)求a1、a2、a3的值，猜想an的表达式，并用数学归纳法证明；
(2)将数列{an}依次按1项、2项、3项、4项循环地分为(a1)，(a2，a3)，(a4，a5，a6)，(a7，a8，a9，a10)；(a11)，(a12，a13)，(a14，a15，a16)，(a17，a18，a19，a20)；(a21)，…，分别计算各个括号内各数之和，设由这些和按原来括号的前后顺序构成的数列为{bn}，求b5＋b100的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，即过P的切线的斜率k＝
，由于P(
＝2，因此切线方程为y－
)且与极轴平行的直线的方程是( )
B．ρsinθ＝