
 ��һ��������EFGH��EH����ֱ����һ��С�ӣ��ջ���߲˿��͵�F���ӱ����ߣ����ǣ��˵طֱ�Ϊ��������S1��S2������S1�е��߲��˵��ӱ߽Ͻ���S2�е��߲��˵�F��Ͻ������˵���S1��S2�ķֽ���C�ϵĵ㵽�ӱ��뵽F��ľ�����ȣ��ֽ���ƽ��ֱ������ϵ������ԭ��OΪEF���е㣬��F������Ϊ��1��0������ͼ
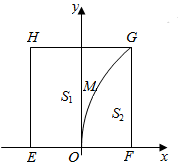
��һ��������EFGH��EH����ֱ����һ��С�ӣ��ջ���߲˿��͵�F���ӱ����ߣ����ǣ��˵طֱ�Ϊ��������S1��S2������S1�е��߲��˵��ӱ߽Ͻ���S2�е��߲��˵�F��Ͻ������˵���S1��S2�ķֽ���C�ϵĵ㵽�ӱ��뵽F��ľ�����ȣ��ֽ���ƽ��ֱ������ϵ������ԭ��OΪEF���е㣬��F������Ϊ��1��0������ͼ���� ��1����ֽ���������һ��Ϊ��x��y�������������������̹�ϵ������⼴�ɣ�
��2����M��x0��y0������y0=1���ֱ������Ӧ��������������FOMGH����������бȽϼ��ɣ�
���  �⣺��1����ֽ���������һ��Ϊ��x��y�����������|x+1|=$\sqrt{��x-1��^{2}+{y}^{2}}$����y=2$\sqrt{x}$����0��x��1����
�⣺��1����ֽ���������һ��Ϊ��x��y�����������|x+1|=$\sqrt{��x-1��^{2}+{y}^{2}}$����y=2$\sqrt{x}$����0��x��1����
��2����M��x0��y0������y0=1��
��x0=$\frac{{{y}_{0}}^{2}}{4}$=$\frac{1}{4}$��
�����������ľ������ΪS3����S3=2����$\frac{1}{4}$+1��=2��$\frac{5}{4}$=$\frac{5}{2}$��
�������EMOGH�����ΪS4����S4=S3-S��OMP+S��MGN=$\frac{5}{2}$-$\frac{1}{2}$��$\frac{1}{4}$��1+$\frac{1}{2}��\frac{3}{4}��1$=$\frac{11}{4}$��
S1-S3=$\frac{8}{3}-\frac{5}{2}$=$\frac{1}{6}$��S4-S1=$\frac{11}{4}$-$\frac{8}{3}$=$\frac{1}{12}$��$\frac{1}{6}$��
�������EMOGH��������ӽ�S1�������
���� ������Ҫ����Բ���ߵĹ켣���⣬����ѧ���������������ۺ��Խ�ǿ���ѶȽϴ�


 Ӯ�ڿ�����ʦ��ʱ�ƻ�ϵ�д�
Ӯ�ڿ�����ʦ��ʱ�ƻ�ϵ�д� �������Ͽ�ʱͬ��ѵ��ϵ�д�
�������Ͽ�ʱͬ��ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1010��2 | B�� | ��12��10 | C�� | ��11��16 | D�� | ��1001��8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | -$\sqrt{3}$+2 | C�� | -$\sqrt{3}$-2 | D�� | $\sqrt{3}$-2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com