
分析 (1)分别根据数列{αn}的前n项和为n2+pn.数列{bn}的前n项和为32n-n2,得到数列{αn}和数列{bn}的通项公式,再根据α10=b10,代值计算即可;
(2)由数列{bn}是以31为首项,以-2为公差的等差数列,可知数列{cn}是以31为首项,以-4为公差的等差数列,即可求出通项公式,
(3)先判断cn从第几项小于0,再分类求出数列{dn}的前n项和Tn.
解答 解:(1)∵数列{αn}的前n项和为n2+pn,
∴αn=n2+pn-(n-1)2-p(n-1)=2n+p-1,
∵数列{bn}的前n项和为32n-n2,
∴bn=32n-n2-32(n-1)+(n-1)2=-2n+33,
∵α10=b10,
∴2×10+p-1=-2×10+33,
∴p=-6,
(2)由(1)可知,bn=-2(n-1)+31,
当n=1时,b1=31,
即数列{bn}是以31为首项,以-2为公差的等差数列,
∵取数列{bn}的第1项.第3项.第5项…构成-个新的数列{cn},
∴数列{cn}是以31为首项,以-4为公差的等差数列,
∴cn=31-4(n-1)=-4n+35,
(3)由(2)可知当cn=-4n+35>0时,解得n≤8,
当cn=-4n+35<0时,解得n≥9,
∵dn=|cn|,
∴n≤8时,Tn=31+27+…+(-4n+35)=$\frac{n(31+35-4n)}{2}$=-2n2+33n
当n≥9时,Tn=31+27+…+3+|-1|+|-5|+…+|-4n+35|=(31+27+…+3)+(1+5+…+4n-35)=$\frac{8(31+3)}{2}$+$\frac{(n-8)(1+4n-35)}{2}$=2n2-33n+272,
综上所述Tn=$\left\{\begin{array}{l}{-2{n}^{2}+33n,n≤8}\\{2{n}^{2}-33n+272,n≥9}\end{array}\right.n∈N*$
点评 本题考查了数列的递推公式和等差的数列的定义以及性质和前n项和公式,属于中档题.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
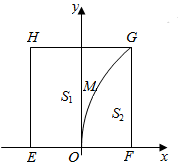 有一块正方形EFGH,EH所在直线是一条小河,收获的蔬菜可送到F点或河边运走.于是,菜地分别为两个区域S1和S2,其中S1中的蔬菜运到河边较近,S2中的蔬菜运到F点较近,而菜地内S1和S2的分界线C上的点到河边与到F点的距离相等,现建立平面直角坐标系,其中原点O为EF的中点,点F的坐标为(1,0),如图
有一块正方形EFGH,EH所在直线是一条小河,收获的蔬菜可送到F点或河边运走.于是,菜地分别为两个区域S1和S2,其中S1中的蔬菜运到河边较近,S2中的蔬菜运到F点较近,而菜地内S1和S2的分界线C上的点到河边与到F点的距离相等,现建立平面直角坐标系,其中原点O为EF的中点,点F的坐标为(1,0),如图查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4{C}_{13}^{2}}{{C}_{52}^{2}}$ | B. | $\frac{{C}_{13}^{2}}{{C}_{52}^{2}}$ | C. | $\frac{2}{52}$ | D. | $\frac{13}{52}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com