
分析 由减函数可知f(x)在两段上均为减函数,且在第一段的最小值大于或等于第二段上的最大值,作出|f(x)|和y=2-$\frac{x}{3}$的图象,根据交点个数判断3a与2的大小关系,列出不等式组解出.
解答 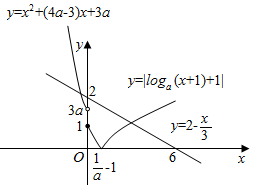 解:∵f(x)是R上的单调递减函数,
解:∵f(x)是R上的单调递减函数,
∴y=x2+(4a-3)x+3a在(-∞.,0)上单调递减,y=loga(x+1)+1在(0,+∞)上单调递减,
且f(x)在(-∞,0)上的最小值大于或等于f(0).
∴$\left\{\begin{array}{l}{\frac{3-4a}{2}≥0}\\{0<a<1}\\{3a≥1}\end{array}\right.$,解得$\frac{1}{3}$≤a≤$\frac{3}{4}$.
作出y=|f(x)|和y=2-$\frac{x}{3}$的函数草图如图所示:
由图象可知|f(x)|=2-$\frac{x}{2}$在[0,+∞)上有且只有一解,
∵|f(x)|=2-$\frac{x}{3}$恰有两个不相等的实数解,
∴x2+(4a-3)x+3a=2-$\frac{x}{3}$在(-∞,0)上只有1解,
即x2+(4a-$\frac{8}{3}$)x+3a-2=0在(-∞,0)上只有1解,
∴$\left\{\begin{array}{l}{(4a-\frac{8}{3})^{2}-4(3a-2)=0}\\{-\frac{4a-\frac{8}{3}}{2}<0}\end{array}\right.$或$\left\{\begin{array}{l}{(4a-\frac{8}{3})^{2}-4(3a-2)>0}\\{3a-2<0}\end{array}\right.$,
解得a=$\frac{51}{36}$或a<$\frac{2}{3}$,
又$\frac{1}{3}$≤a≤$\frac{3}{4}$,∴$\frac{1}{3}≤a<\frac{2}{3}$.
故答案为[$\frac{1}{3}$,$\frac{2}{3}$).
点评 本题考查了分段函数的单调性,函数零点的个数判断,结合函数函数图象判断端点值的大小是关键,属于中档题.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:解答题
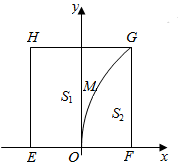 有一块正方形EFGH,EH所在直线是一条小河,收获的蔬菜可送到F点或河边运走.于是,菜地分别为两个区域S1和S2,其中S1中的蔬菜运到河边较近,S2中的蔬菜运到F点较近,而菜地内S1和S2的分界线C上的点到河边与到F点的距离相等,现建立平面直角坐标系,其中原点O为EF的中点,点F的坐标为(1,0),如图
有一块正方形EFGH,EH所在直线是一条小河,收获的蔬菜可送到F点或河边运走.于是,菜地分别为两个区域S1和S2,其中S1中的蔬菜运到河边较近,S2中的蔬菜运到F点较近,而菜地内S1和S2的分界线C上的点到河边与到F点的距离相等,现建立平面直角坐标系,其中原点O为EF的中点,点F的坐标为(1,0),如图查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 废品率x | 1.3 | 1.5 | 1.6 | 1.7 | 1.9 |
| 利润y | 150 | 120 | 110 | 100 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{2}$) | B. | (-∞,$\frac{1}{2}$)∪($\frac{3}{2}$,+∞) | C. | ($\frac{1}{2}$,$\frac{3}{2}$) | D. | ($\frac{3}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
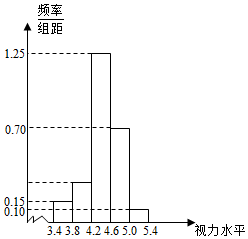 为了了解学生的视力情况,随机抽查了一批学生的视力,将抽查结果绘制成频率分布直方图(如图所示).若在[5.0,5.4]内的学生人数是4,则根据图中数据可得样本数据在[3.8,4.2)内的人数是12.
为了了解学生的视力情况,随机抽查了一批学生的视力,将抽查结果绘制成频率分布直方图(如图所示).若在[5.0,5.4]内的学生人数是4,则根据图中数据可得样本数据在[3.8,4.2)内的人数是12.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com