
分析 由题意X~N(0,22),求得P(|X|≤4)=P(-4≤X≤4)=0.954 4.设Y表示5件产品中合格品个数,则Y~B(5,0.954 4).由此能求出生产的5件产品的合格率不小于80%的概率.
解答 解 由题意X~N(0,22),求得P(|X|≤4)=P(-4≤X≤4)=0.954 4.
设Y表示5件产品中合格品个数,则Y~B(5,0.954 4).
∴P(Y≥5×0.8)=P(Y≥4)=${C}_{5}^{4}$×(0.9544)4×0.045 6+${C}_{5}^{5}$×(0.9544)5≈0.1892+0.7919≈0.981.
故生产的5件产品的合格率不小于80%的概率约为0.981.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意正态分布和二项分布的合理运用.


 培优三好生系列答案
培优三好生系列答案科目:高中数学 来源: 题型:解答题
 如图所示,在三棱柱ABC-A'B'C'中,AA'⊥底面ABC,AB=BC=AA',∠ABC=90°,O是侧面ABB'A'的中心,点D、E、F分别是棱A'C'、AB、BB'的中点.
如图所示,在三棱柱ABC-A'B'C'中,AA'⊥底面ABC,AB=BC=AA',∠ABC=90°,O是侧面ABB'A'的中心,点D、E、F分别是棱A'C'、AB、BB'的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e2017•f(2017)>f(0) | B. | e2017•f(2017)=f(0) | ||
| C. | e2017•f(2017)<f(0) | D. | e2017f(2017)与f(0)的大小无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
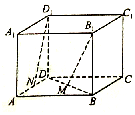 如图所示,在正方体ABCD-A1B1C1D1中,已知棱长为a,M,N分别是BD和AD的中点,则B1M与D1N所成角的余弦值为( )
如图所示,在正方体ABCD-A1B1C1D1中,已知棱长为a,M,N分别是BD和AD的中点,则B1M与D1N所成角的余弦值为( )| A. | $\frac{\sqrt{30}}{10}$ | B. | $\frac{\sqrt{30}}{10}$a | C. | -$\frac{\sqrt{30}}{10}$ | D. | $\frac{\sqrt{15}}{15}$a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com