
| A. | ①③ | B. | ②④ | C. | ②③④ | D. | ①②③④ |
分析 逐项分析误即可.①由集合的表示法可以判断;②定义域为R,即分母恒不为零,a=0时不成立,利用判别式可得;③利用奇偶性的判别方法可知;④利用二次函数的图象即可判断.
解答 解:①∵集合A,B都为点集,故{2,3}表示错误,应为{(2,3)};
②当a=0时,显然定义域不是R,当a等于零时,分母恒不为0,
所以△=1+12a<0,得:$a<-\frac{1}{12}$,故②正确;
③因为定义域不关于原点对称,所以函数f(x)不具奇偶性,故③错误;
④函数的图象开口向下,对称轴为$x=\frac{3}{2}$,所以函数在(2,+∞)上递减,故④正确.
综上所述,答案为②④,
故选B.
点评 本题考查了集合的表示法和函数的相关知识.正确掌握它们的表示方法和求解方法是解题的关键.①③容易判断出错.属于易错题.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
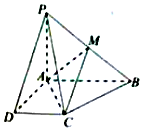 如图,在四棱锥P-ABCD中,已知AB∥CD,PA=AB=AD=2,DC=1,AD⊥AB,PD=PB=2$\sqrt{2}$.点M是PB的中点.
如图,在四棱锥P-ABCD中,已知AB∥CD,PA=AB=AD=2,DC=1,AD⊥AB,PD=PB=2$\sqrt{2}$.点M是PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9x-y-4=0 | B. | x+y+5=0 | C. | 2x+y-2=0 | D. | 9x+y-5=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 甲厂高 | B. | 乙厂高 | ||
| C. | 甲、乙两厂相等 | D. | 甲、乙两厂高低无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com