
| A. | 9x-y-4=0 | B. | x+y+5=0 | C. | 2x+y-2=0 | D. | 9x+y-5=0 |
分析 设过点P的弦与椭圆交于A,B两点,并设出他们的坐标,代入椭圆方程联立,两式相减,根据中点P的坐标可知x1+x2和y1+y2的值,进而求得直线AB的斜率,根据点斜式即可求得直线的方程.
解答 解:设这条弦的两端点为A(x1,y1),B(x2,y2),斜率为k,
∴$\left\{\begin{array}{l}{\frac{{y}_{1}^{2}}{9}+{x}_{1}^{2}=1}\\{\frac{{y}_{2}^{2}}{9}+{x}_{2}^{2}=1}\end{array}\right.$,两式相减可得:$\frac{{(y}_{1}+{y}_{2})({y}_{1}-{y}_{2})}{9}$+(x1+x2)(x1-x2)=0,
由中点坐标公式可得:x1+x2=1,y1+y2=1,
∴y1-y2=-9(x1-x2),
由k=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=-9,
∴弦所在的直线方程y-$\frac{1}{2}$=-9(x-$\frac{1}{2}$),整理得:9x+y-5=0,
故选:D.
点评 本题主要考查了椭圆的简单性质和直线与椭圆的位置关系,考查弦长的中点坐标公式,考查“点差法”应用,直线的点斜式方程,考查计算能力,属于中档题.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直线和直线外一点确定一个平面 | |
| B. | 过不在一条直线上的三点,有且只有一个平面 | |
| C. | 空间中如果两个角的两边分别对应平行,那么这两个角相等或互补 | |
| D. | 平行于同一个平面的两个平面相互平行 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ②④ | C. | ②③④ | D. | ①②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
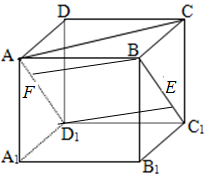 如图,棱长为1的正方体ABCD-A1B1C1D1中,E,F是侧面对角线BC1,AD1上一点,若BED1F是菱形,则其在底面ABCD上投影的四边形面积( )
如图,棱长为1的正方体ABCD-A1B1C1D1中,E,F是侧面对角线BC1,AD1上一点,若BED1F是菱形,则其在底面ABCD上投影的四边形面积( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{3-\sqrt{2}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com