
ĄŸÌâÄżĄżÎȘÁËœâÆß°àѧÉúÏČ°źŽòÀșÇòÊÇ·ńÓëĐÔ±đÓĐčŰŁŹ¶Ô±Ÿ°à50ÈËœűĐĐÁËÎÊŸí”śČé”Ă”œÁËÈçÏ”ÄÁĐÁȘ±íŁș
ÏČ°źŽòÀșÇò | Č»ÏČ°źŽòÀșÇò | șÏ | |
ÄĐÉú | 5 | ||
ĆźÉú | 10 | ||
șÏŒÆ | 50 |
ÒŃÖȘÔÚÈ«Čż50ÈËÖĐËæ»úłéÈĄ1ÈËłé”œÏČ°źŽòÀșÇò”ÄѧÉú”ÄžĆÂÊÎȘ![]() Łź
Łź
Łš1Ł©Ç뜫ÉÏĂæ”ÄÁĐÁȘ±íČčłäÍêŐû(Č»ÓĂĐŽŒÆËăčęłÌ)Ł»
Łš2Ł©ÄÜ·ńÔÚ·žŽíÎó”ÄžĆÂÊČ»łŹčę0.005”ÄÇ°ÌáÏÂÈÏÎȘÏČ°źŽòÀșÇòÓëĐÔ±đÓĐčŰŁżË”ĂśÄă”ÄÀíÓÉŁ»
Łš3Ł©ÏÖŽÓĆźÉúÖĐłéÈĄ2ÈËœűÒ»Čœ”śČ飏ÉèÆäÖĐÏČ°źŽòÀșÇò”ÄĆźÉúÈËÊęÎȘ![]() ŁŹÇó
ŁŹÇó![]() ”Ä·ÖČŒÁĐÓëÆÚÍû.
”Ä·ÖČŒÁĐÓëÆÚÍû.
ÏÂĂæ”ÄÁÙœçÖ”±íč©ČÎżŒŁș
| 0.15 | 0.10 | 0.05[ | 0.025 | 0.01 | 0.005 | 0.001 |
| 2.072 | 2.70 | 3.841 | 5.024 | 6.635 | 7.879 | 10.82 |
(ČÎżŒč«ÊœŁș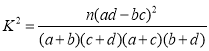 ŁŹÆäÖĐ
ŁŹÆäÖĐ![]() )
)![]()
ĄŸŽđ°žĄżŁš1Ł©ŒûœâÎöŁš2Ł©ÄÜŁš3Ł©![]()
ĄŸœâÎöĄż
œâŁș(1) ÁĐÁȘ±íČčłäÈçÏÂŁș-
ÏČ°źŽòÀșÇò | Č»ÏČ°źŽòÀșÇò | șÏŒÆ | |
ÄĐÉú | 20 | 5 | 25 |
ĆźÉú | 10 | 15 | 25 |
șÏŒÆ | 30 | 20 | 50 |
Łš2Ł©Ąß![]()
ĄàÔÚ·žŽíÎó”ÄžĆÂÊČ»łŹčę0.005”ÄÇ°ÌáÏÂŁŹÈÏÎȘÏČ°źŽòÀșÇòÓëĐÔ±đÓĐčŰ.
Łš3Ł©ÏČ°źŽòÀșÇò”ÄĆźÉúÈËÊę![]() ”ÄżÉÄÜÈĄÖ”ÎȘ
”ÄżÉÄÜÈĄÖ”ÎȘ![]() .
.
ÆäžĆÂÊ·Ö±đÎȘ![]() ,
,![]() ,
,![]()
čÊ![]() ”Ä·ÖČŒÁĐÎȘ:
”Ä·ÖČŒÁĐÎȘ:
|
|
|
|
|
|
|
|
![]() ”ÄÆÚÍûÖ”ÎȘ:
”ÄÆÚÍûÖ”ÎȘ:![]()
±ŸÌâÊÇÒ»žöÍłŒÆŚÛșÏÌ⣏°üșŹ¶ÀÁąĐÔŒìŃ饹ÀëÉąĐÍËæ»ú±äÁż”ÄÆÚÍûÓë·œČîșÍžĆÂÊŁŹ±ŸÌâÍščꎎÉèÇéŸłŒ€·ąŃ§ÉúŃ§Ï°Êęѧ”ÄÇéžĐŁŹ°ïÖúĆàŃűÆäŃÏœśÖÎѧ”ÄÌŹ¶ÈŁź
Łš1Ł©žùŸĘÔÚÈ«Čż50ÈËÖĐËæ»úłéÈĄ1ÈËłé”œÏČ°źŽòÀșÇò”ÄѧÉú”ÄžĆÂÊŁŹŚöłöÏČ°źŽòÀșÇò”ÄÈËÊ꣏œű¶űŚöłöÄĐÉú”ÄÈËÊ꣏ÌîșñížńŁź
Łš2Ł©žùŸĘËùžű”Äč«ÊœŁŹŽúÈëÊęŸĘÇółöÁÙœçÖ”ŁŹ°ŃÇó”Ă”ÄœáčûÍŹÁÙœçÖ”±íœűĐĐ±ÈœÏŁŹżŽłöÓжàŽó”Ä°ŃÎŐ˔ÜŽòÀșÇòșÍĐÔ±đÓĐčŰÏ”Łź
Łš3Ł©ÏČ°źŽòÀșÇò”ÄĆźÉúÈËÊęŠÎ”ÄżÉÄÜÈĄÖ”ÎȘ0ŁŹ1ŁŹ2ŁŹÍščęÁĐŸÙ”Ă”œÊÂŒțÊ꣏·Ö±đŒÆËăłöËüĂǔĞĆÂÊŁŹŚîșóÀûÓĂÁĐłö·ÖČŒÁĐŁŹÇółöÆÚÍûŒŽżÉŁź
œâŁș(1) ÁĐÁȘ±íČčłäÈçÏÂŁș----------------------------------------3·Ö
ÏČ°źŽòÀșÇò | Č»ÏČ°źŽòÀșÇò | șÏŒÆ | |
ÄĐÉú | 20 | 5 | 25 |
ĆźÉú | 10 | 15 | 25 |
șÏŒÆ | 30 | 20 | 50 |
Łš2Ł©Ąß![]() ------------------------6·Ö
------------------------6·Ö
ĄàÔÚ·žŽíÎó”ÄžĆÂÊČ»łŹčę0.005”ÄÇ°ÌáÏÂŁŹÈÏÎȘÏČ°źŽòÀșÇòÓëĐÔ±đÓĐčŰ.---------------------7·Ö
Łš3Ł©ÏČ°źŽòÀșÇò”ÄĆźÉúÈËÊę![]() ”ÄżÉÄÜÈĄÖ”ÎȘ
”ÄżÉÄÜÈĄÖ”ÎȘ![]() .-------------------------9·Ö
.-------------------------9·Ö
ÆäžĆÂÊ·Ö±đÎȘ![]() ,
,![]() ,
,![]()
--------------------------12·Ö
čÊ![]() ”Ä·ÖČŒÁĐÎȘ:
”Ä·ÖČŒÁĐÎȘ:
|
|
|
|
|
|
|
|
--------------------------13·Ö
![]() ”ÄÆÚÍûÖ”ÎȘ:
”ÄÆÚÍûÖ”ÎȘ:![]() ---------------------14·Ö
---------------------14·Ö


 ÌìÌìÏòÉÏÒ»±ŸșĂŸíÏ”ÁĐŽđ°ž
ÌìÌìÏòÉÏÒ»±ŸșĂŸíÏ”ÁĐŽđ°ž ХѧÉú10·ÖÖÓÓŠÓĂÌâÏ”ÁĐŽđ°ž
ХѧÉú10·ÖÖÓÓŠÓĂÌâÏ”ÁĐŽđ°ž
| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒŃÖȘŒŻșÏAŁœ{x|![]() 0}ŁŹBŁœ{x|x2©3x+2ŁŒ0}ŁŹUŁœRŁŹÇó
0}ŁŹBŁœ{x|x2©3x+2ŁŒ0}ŁŹUŁœRŁŹÇó
Łš1Ł©AĄÉBŁ»
Łš2Ł©AĄÈBŁ»
Łš3Ł©ŁšUAŁ©ĄÉBŁź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒŃÖȘ![]() ÎȘ¶šÒćÔÚÊ”ÊęŒŻ
ÎȘ¶šÒćÔÚÊ”ÊęŒŻ![]() ÉÏ”ÄșŻÊ꣏°Ń·œłÌ
ÉÏ”ÄșŻÊ꣏°Ń·œłÌ![]() łÆÎȘșŻÊę
łÆÎȘșŻÊę![]() ”ÄÌŰŐś·œłÌŁŹÌŰŐś·œłÌ”ÄÁœžöÊ”žù
”ÄÌŰŐś·œłÌŁŹÌŰŐś·œłÌ”ÄÁœžöÊ”žù![]() Ąą
Ąą![]() Łš
Łš![]() Ł©ŁŹłÆÎȘ
Ł©ŁŹłÆÎȘ![]() ”ÄÌŰŐśžù.
”ÄÌŰŐśžù.
Łš1Ł©ÌÖÂÛșŻÊę![]() ”ÄÆæĆŒĐÔŁŹČąË”ĂśÀíÓÉŁ»
”ÄÆæĆŒĐÔŁŹČąË”ĂśÀíÓÉŁ»
Łš2Ł©ÒŃÖȘ![]() ÎȘžű¶šÊ”Ê꣏Çó
ÎȘžű¶šÊ”Ê꣏Çó![]() ”ıíŽïÊœŁ»
”ıíŽïÊœŁ»
Łš3Ł©°ŃșŻÊę![]() ŁŹ
ŁŹ![]() ”ÄŚîŽóÖ”ŒÇŚś
”ÄŚîŽóÖ”ŒÇŚś![]() ŁŹŚîĐĄÖ”ŒÇŚś
ŁŹŚîĐĄÖ”ŒÇŚś![]() ŁŹŃĐŸżșŻÊę
ŁŹŃĐŸżșŻÊę![]() ŁŹ
ŁŹ![]() ”Ä”„”śĐÔŁŹÁî
”Ä”„”śĐÔŁŹÁî![]() ŁŹÈô
ŁŹÈô![]() șăłÉÁąŁŹÇó
șăłÉÁąŁŹÇó![]() ”ÄÈĄÖ”·¶Î§.
”ÄÈĄÖ”·¶Î§.
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒŃÖȘ![]() ”ÄÒ»žöÄÚœÇÎȘ
”ÄÒ»žöÄÚœÇÎȘ![]() ŁŹČąÇÒÈę±ßł€ččłÉč«ČîÎȘ4”Ä”ÈČîÊęÁĐ,Ôò
ŁŹČąÇÒÈę±ßł€ččłÉč«ČîÎȘ4”Ä”ÈČîÊęÁĐ,Ôò![]() ”ÄĂæ»ęÎȘŁš Ł©
”ÄĂæ»ęÎȘŁš Ł©
A. 15 B. ![]() C.
C. ![]() D.
D. ![]()
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚÈęÀ⌶![]() ÖĐŁŹ
ÖĐŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ÎȘÏ߶Î
ÎȘÏ߶Î![]() ”ÄÖД㣏
”ÄÖД㣏![]() ÊÇÏ߶Î
ÊÇÏ߶Î![]() ÉÏÒ»¶Ż”㣟
ÉÏÒ»¶Ż”㣟

Łš1Ł©”±![]() ʱŁŹÇóÖ€Łș
ʱŁŹÇóÖ€Łș![]() Ăæ
Ăæ![]() Ł»
Ł»
Łš2Ł©”±![]() ”ÄĂæ»ęŚîĐĄÊ±ŁŹÇóÈęÀ⌶
”ÄĂæ»ęŚîĐĄÊ±ŁŹÇóÈęÀ⌶![]() ”ÄÌć»ęŁź
”ÄÌć»ęŁź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒŃÖȘșŻÊę![]() ŁŹÆäÖĐaÎȘÊ”Êę.
ŁŹÆäÖĐaÎȘÊ”Êę.
Łš1Ł©”±a=-1ʱŁŹÇóșŻÊęy=f(x)”ÄÁă”㣻
Łš2Ł©Èôf(x)ÔÚŁš-2,2Ł©ÉÏÎȘÔöșŻÊ꣏ÇóÊ”Êęa”ÄÈĄÖ”·¶Î§Ł»
Łš3Ł©¶ÔÓÚžű¶š”ÄÊ”ÊęaŁŹÈôŽæÔÚÁœžöČ»Ïà”È”ÄÊ”Êęžù![]() ŁŹ
ŁŹ![]() ŁŹŁš
ŁŹŁš![]() <
<![]() ÇÒ
ÇÒ![]() ĄÙ0Ł©Êč”Ăf(
ĄÙ0Ł©Êč”Ăf(![]() )=f(
)=f(![]() ),Çó
),Çó![]() ”ÄÈĄÖ”·¶Î§.
”ÄÈĄÖ”·¶Î§.
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒŃÖȘșŻÊęf(x)Łœ|2xŁ1|Ł«|xŁ2a|.
(1)”±aŁœ1ʱŁŹÇóf(x)ĄÜ3”ÄœâŒŻŁ»
(2)”±xĄÊ[1ŁŹ2]ʱŁŹf(x)ĄÜ3șăłÉÁąŁŹÇóÊ”Êęa”ÄÈĄÖ”·¶Î§Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒŃÖȘÖ±Ïßlčę”ăPŁš1ŁŹ2Ł©ŁŹžùŸĘÏÂÁĐÌőŒț·Ö±đÇółöÖ±Ïßl”Ä·œłÌŁšĐ±œŰÊœ·œłÌŁ©Łș
Łš1Ł©Ö±ÏßlÓë![]() ŽčÖ±Ł»
ŽčÖ±Ł»
Łš2Ł©lÔÚxÖ᥹yÖáÉÏ”ÄœŰŸàÖźșÍ”ÈÓÚ0Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚ¶àĂæÌć![]() ÖĐŁŹ
ÖĐŁŹ![]() ÆœĂæ
ÆœĂæ![]() ŁŹÇÒ
ŁŹÇÒ![]() ÊDZ߳€ÎȘ2”ĔȱßÈęœÇĐÎŁŹ
ÊDZ߳€ÎȘ2”ĔȱßÈęœÇĐÎŁŹ![]() Łź
Łź

Łš1Ł©Èô![]() ÊÇÏ߶Î
ÊÇÏ߶Î![]() ”ÄÖД㣏րÜŁșÖ±Ïß
”ÄÖД㣏րÜŁșÖ±Ïß![]() Ăæ
Ăæ![]() Ł»
Ł»
Łš2Ł©Çó¶țĂæœÇ![]() ”ÄÆœĂæœÇ”ÄÓàÏÒÖ”Łź
”ÄÆœĂæœÇ”ÄÓàÏÒÖ”Łź
Č鿎Žđ°žșÍœâÎö>>
čúŒÊѧУÓĆŃĄ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com