
【题目】已知函数![]() ,其中a为实数.
,其中a为实数.
(1)当a=-1时,求函数y=f(x)的零点;
(2)若f(x)在(-2,2)上为增函数,求实数a的取值范围;
(3)对于给定的实数a,若存在两个不相等的实数根![]() ,
,![]() ,(
,(![]() <
<![]() 且
且![]() ≠0)使得f(
≠0)使得f(![]() )=f(
)=f(![]() ),求
),求![]() 的取值范围.
的取值范围.
【答案】(1)函数y=f(x)的零点为![]() 或
或![]() ;(2)见解析
;(2)见解析
【解析】
(1)直接解方程即得函数y=f(x)的零点为![]() 或
或![]() ;(2)由题得
;(2)由题得![]() ,利用分段函数的单调性和二次函数的图象分析即得解;(3)对
,利用分段函数的单调性和二次函数的图象分析即得解;(3)对![]() 分三种情况讨论,结合函数的图象分析得解.
分三种情况讨论,结合函数的图象分析得解.
(1)![]() ,
,
所以![]() 或
或![]() ,
,
所以![]() 或
或![]() ,
,
所以![]() 或
或![]() .
.
所以函数y=f(x)的零点为![]() 或
或![]() .
.
(2)由题得![]() ,二次函数的对称轴为
,二次函数的对称轴为![]() ,
,
当![]() 即
即![]() 时,由题得
时,由题得![]() ,即
,即![]() .因为
.因为![]() ,所以
,所以![]() ;
;
当![]() 即
即![]() 时,函数
时,函数![]() 在(-2,2)上为增函数,所以
在(-2,2)上为增函数,所以![]() ;
;
当![]() 即
即![]() 时,由题得
时,由题得![]() ,所以
,所以![]() ,所以
,所以![]() .
.
综上,所以实数a的取值范围为![]() .
.
(3)当![]() 时,
时,![]() ,
,
![]() (因为
(因为![]() <
<![]() 且
且![]() ≠0,所以不能取等)
≠0,所以不能取等)
当![]() 时,函数在R上单调递增,所以不满足题意;
时,函数在R上单调递增,所以不满足题意;
当![]() 时,函数在
时,函数在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
所以![]() ,令
,令![]() ,
,
①若![]() ,则
,则![]() ,由
,由![]() 知
知![]() 且
且![]()
所以![]()
所以函数M在![]() 上是增函数,
上是增函数,
所以![]() ,
,
所以此时![]() .
.
②若![]() ,则
,则![]() ,则
,则![]() ,
,![]()
所以![]() ,因为
,因为![]() ,
,![]() ,所以
,所以![]()
![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
令![]() ,所以
,所以![]()
所以![]() ,
,
综上,当![]() 时,
时,![]() ;当
;当![]() 时,不存在;当
时,不存在;当![]() 时,
时,![]() .
.


科目:高中数学 来源: 题型:
【题目】华为手机作为华为公司三大核心业务之一,2018年的销售量跃居全球第二名,某机构随机选取了100名华为手机的顾客进行调查,并将这![]() 人的手机价格按照
人的手机价格按照![]() ,
,![]() ,…
,…![]() 分成
分成![]() 组,制成如图所示的频率分布直方图,其中
组,制成如图所示的频率分布直方图,其中![]() 是
是![]() 的
的![]() 倍.
倍.

(1)求![]() ,
,![]() 的值;
的值;
(2)求这![]() 名顾客手机价格的平均数(同一组中的数据用该组区间的中间值作代表);
名顾客手机价格的平均数(同一组中的数据用该组区间的中间值作代表);
(3)利用分层抽样的方式从手机价格在![]() 和
和![]() 的顾客中选取
的顾客中选取![]() 人,并从这
人,并从这![]() 人中随机抽取
人中随机抽取![]() 人进行回访,求抽取的
人进行回访,求抽取的![]() 人手机价格在不同区间的概率.
人手机价格在不同区间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,
中,![]() 平面
平面![]() ,且底面
,且底面![]() 为边长为2的菱形,
为边长为2的菱形,![]() ,
,![]() .
.
(Ⅰ)记![]() 在平面
在平面![]() 内的射影为
内的射影为![]() (即
(即![]() 平面
平面![]() ),试用作图的方法找出M点位置,并写出
),试用作图的方法找出M点位置,并写出![]() 的长(要求写出作图过程,并保留作图痕迹,不需证明过程和计算过程);
的长(要求写出作图过程,并保留作图痕迹,不需证明过程和计算过程);

(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解七班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
喜爱打篮球 | 不喜爱打篮球 | 合 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为![]() .
.
(1)请将上面的列联表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由;
(3)现从女生中抽取2人进一步调查,设其中喜爱打篮球的女生人数为![]() ,求
,求![]() 的分布列与期望.
的分布列与期望.
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05[ | 0.025 | 0.01 | 0.005 | 0.001 |
| 2.072 | 2.70 | 3.841 | 5.024 | 6.635 | 7.879 | 10.82 |
(参考公式: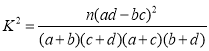 ,其中
,其中![]() )
)![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在![]() 上的函数
上的函数![]() ,如果对于任意的
,如果对于任意的![]() ,存在常数
,存在常数![]() 都有
都有![]() 成立,则称
成立,则称![]() 为函数
为函数![]() 在
在![]() 上的一个上界.已知函数
上的一个上界.已知函数![]() .
.
(1)当![]() 时,试判断函数
时,试判断函数![]() 在
在![]() 上是否存在上界,若存在请求出该上界,若不存在请说明理由;
上是否存在上界,若存在请求出该上界,若不存在请说明理由;
(2)若函数![]() 在
在![]() 上的上界为3,求出实数
上的上界为3,求出实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com