
【题目】对于定义在![]() 上的函数
上的函数![]() ,如果对于任意的
,如果对于任意的![]() ,存在常数
,存在常数![]() 都有
都有![]() 成立,则称
成立,则称![]() 为函数
为函数![]() 在
在![]() 上的一个上界.已知函数
上的一个上界.已知函数![]() .
.
(1)当![]() 时,试判断函数
时,试判断函数![]() 在
在![]() 上是否存在上界,若存在请求出该上界,若不存在请说明理由;
上是否存在上界,若存在请求出该上界,若不存在请说明理由;
(2)若函数![]() 在
在![]() 上的上界为3,求出实数
上的上界为3,求出实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】某河流上的一座水力发电站,每年六月份的发电量![]() (单位:万千瓦时)与该河上游在六月份的降雨量
(单位:万千瓦时)与该河上游在六月份的降雨量![]() (单位:毫米)有关据统计,当
(单位:毫米)有关据统计,当![]() 时,
时, ![]() ;
; ![]() 每增加10,
每增加10, ![]() 增加5.已知近20年
增加5.已知近20年![]() 的值为:140,110,160,70,200,160,140,160,220,200,110,160,160,200,140,110,160,220,140,160.
的值为:140,110,160,70,200,160,140,160,220,200,110,160,160,200,140,110,160,220,140,160.
(1)完成如下的频率分布表:近20年六月份降雨量频率分布表

(2)假定今年六月份的降雨量与近20年六月份降雨量的分布规律相同,并将频率视为概率,求今年六月份该水力发电站的发电量低于490(万千瓦时)或超过530(万千瓦时)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中a为实数.
,其中a为实数.
(1)当a=-1时,求函数y=f(x)的零点;
(2)若f(x)在(-2,2)上为增函数,求实数a的取值范围;
(3)对于给定的实数a,若存在两个不相等的实数根![]() ,
,![]() ,(
,(![]() <
<![]() 且
且![]() ≠0)使得f(
≠0)使得f(![]() )=f(
)=f(![]() ),求
),求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数![]() 的导函数
的导函数![]() 的图象如图所示,则以下关于函数
的图象如图所示,则以下关于函数![]() 的判断:
的判断:
①在区间![]() 内单调递增;
内单调递增;
②在区间![]() 内单调递减;
内单调递减;
③在区间![]() 内单调递增;
内单调递增;
④![]() 是极小值点;
是极小值点;
⑤![]() 是极大值点.
是极大值点.
其中正确的是( )
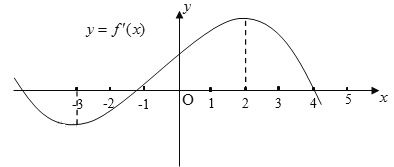
A. ③⑤B. ②③C. ①④⑤D. ①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com