练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．不等式x2（x2+2x+1）＞2x（x2+2x+1）的解集为（-∞，-1）∪（-1，0）∪（2，+∞）．

    分析 原不等式等价于x（x+1）2（x-2）＞0，当x=-1时，不等式不成立，当x≠-1时，不等式等价于x（x-2）＞0，解得x＜0或x＞2且x≠-1，问题得以解决．

    解答 解：x2（x2+2x+1）＞2x（x2+2x+1）等价于x（x+1）2（x-2）＞0，
    当x=-1时，不等式不成立，
    当x≠-1时，不等式等价于x（x-2）＞0，解得x＜0或x＞2且x≠-1，
    故不等式的解集为（-∞，-1）∪（-1，0）∪（2，+∞），
    故答案为：（-∞，-1）∪（-1，0）∪（2，+∞）．

    点评 本题考查了高次不等式的解法，分类讨论是关键，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    16．已知sinx=$\frac{3}{5}$，其中0≤x≤$\frac{π}{2}$．
    （1）求cosx，tanx的值；
    （2）求$\frac{sin（-x）}{{cos（\frac{π}{2}-x）+cos（2π-x）}}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．直线y=2x的参数方程是（　　）
    A．$\left\{{\begin{array}{l}{x=\sqrt{t}}\\{y=2\sqrt{t}}\end{array}}\right.$B．$\left\{{\begin{array}{l}{x=2t+1}\\{y=4t+1}\end{array}}\right.$C．$\left\{{\begin{array}{l}{x=cosθ}\\{y=2sinθ}\end{array}}\right.$D．$\left\{{\begin{array}{l}{x=tanθ}\\{y=2tanθ}\end{array}}\right.$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．设f（x）=x2cosθ-x（1-x）+（1-x）2sinθ在x∈[0，1]时，f（x）＞0恒成立．
    （1）求证：sinθ＞0，cosθ＞0；          
    （2）求θ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．对于任意的实数a，b，c，下列命题正确的是（　　）
    A．若a＞b，c=0，则ac＞bcB．若ac2＞bc2，则a＞b
    C．若a＞b，则$\frac{1}{a}$＞$\frac{1}{b}$D．若a＞b，则ac2＞bc2
    E．若a＞b，则ac2＞bc2   

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．将语文、数学、物理、化学四本书任意地排放在书架的同一层上，计算：
    （1）语文书在数学书的左边的概率是多少？
    （2）化学书在语文书的右边，语文书在物理书的右边的概率是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．（1）函数f（x）=ax2+bx满足：1≤f（1）≤2，2≤f（-2）≤4，求f（-1）的取值范围．
    （2）若不等式ax2-ax+1≥0对x∈R恒成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

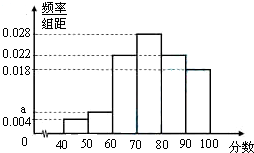    15．某企业为了解下属某部门对本企业职工的服务情况，随机访问50名职工，根据这50名职工对该部门的评分，绘制频率分布直方图（如图所示），其中样本数据分组区间为[40，50），[50，60），…，[80，90），[90，100]
    （1）求频率分布直方图中a的值；
    （2）估计该企业的职工对该部门评分不低于80的概率；
    （3）从评分在[40，60）的受访职工中，随机抽取2人，求此2人的评分恰好有一人在[40，50）的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

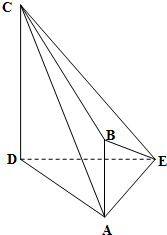    16．如图，在四棱锥E-ABCD中，AE⊥DE，CD⊥平面ADE，AB⊥平面ADE，CD=DA=6，AB=2，DE=3．
    （Ⅰ）求证：平面ACE⊥平面CDE；
    （Ⅱ）求平面CED与平面BEC所成锐二面角的余弦值．

    查看答案和解析>>

    同步练习册答案