
分析 由题意可得x=1为方程的一个根,则方程的另一个根为x>0且x≠1,若k=1,推出方程只有一解x=1;讨论x>1,0<x<1,分离参数k,求出右边函数的范围和单调性,即可得到所求k的范围.
解答 解:关于x的方程kx2-2lnx-k=0,
显然x=1,k-2ln1-k=0成立;
则方程的另一个根为x>0且x≠1,
若k=1,则方程为x2-2lnx-1=0,
由y=x2-2lnx-1,导数为2x-$\frac{2}{x}$=$\frac{2(x+1)(x-1)}{x}$,
可得x=1为极小值点也为最小值点,
则x2-2lnx-1=0只有一解x=1.
当x>1时,方程可化为k=$\frac{2lnx}{{x}^{2}-1}$,
由f(x)=$\frac{2lnx}{{x}^{2}-1}$,x>1,
f′(x)=$\frac{2x-\frac{2}{x}-4xlnx}{({x}^{2}-1)^{2}}$,
令g(x)=2x-$\frac{2}{x}$-4xlnx,x>1,
可得g′(x)=2+$\frac{2}{{x}^{2}}$-4(1+lnx)=$\frac{2}{{x}^{2}}$-2-4lnx,
显然g′(x)在x>1递减,即有g′(x)<g′(1)=0,
则g(x)在x>1递减,即有g(x)<g(1)=0,
即有f(x)在(1,+∞)递减;
同样当0<x<1时,f(x)递减,
且有f(x)>0在x>0且x≠1恒成立,
则当k>0且k≠1时,原方程有两个不等实根.
故答案为:(0,1)∪(1,+∞).
点评 本题考查方程的根的情况,注意运用参数分离和分类讨论的思想方法,以及构造函数法,考查函数的单调性,以及运算能力,属于中档题.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {m|-2≤m≤1} | B. | {m|-$\frac{1}{2}$≤m≤1} | C. | {m|-1≤m≤$\frac{1}{2}$} | D. | {m|-$\frac{1}{2}$≤m≤$\frac{1}{4}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3•21008-3 | B. | 22016-1 | C. | 22009-3 | D. | 22008-3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
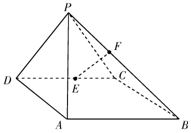 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是平行四边形,∠ABC=45°,AD=AP=2,$AB=DP=2\sqrt{2}$,E为CD的中点,点F在线段PB上.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是平行四边形,∠ABC=45°,AD=AP=2,$AB=DP=2\sqrt{2}$,E为CD的中点,点F在线段PB上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com