
分析 根据题意,先由奇函数的性质可得f(0)=0,再设x>0,则-x<0,由函数的解析式可得f(-x)=(-x)[1-(-x)]=-x(1+x),结合函数的奇偶性可得x>0时,f(x)的解析式,综合三种情况即可得答案.
解答 解:根据题意,f(x)是定义域为R的奇函数,则有f(0)=0,
设x>0,则-x<0,
则f(-x)=(-x)[1-(-x)]=-x(1+x),
又由f(x)是奇函数,则有f(-x)=-f(x),
则有x>0时,f(x)=-f(-x)=x(1+x),
综合可得:f(x)=$\left\{\begin{array}{l}{x(1-x),x<0}\\{0,x=0}\\{x(1+x),x>0}\end{array}\right.$;
故答案为:f(x)=$\left\{\begin{array}{l}{x(1-x),x<0}\\{0,x=0}\\{x(1+x),x>0}\end{array}\right.$.
点评 本题考查函数解析式的求法,利用函数奇偶性的对称性是解决本题的关键,不能忽略f(0)=0.


科目:高中数学 来源: 题型:解答题
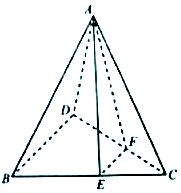 如图,在三棱锥A-BCD中,E,F分别为BC,CD上的点,且BD∥平面AEF.
如图,在三棱锥A-BCD中,E,F分别为BC,CD上的点,且BD∥平面AEF.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com